Определение: Модулем (абсолютной величиной) действительного числа а называется неотрицательное число, взятое из двух чисел а или –а.
Обозначение модуля числа: | а | .
Из определения следует: | а | =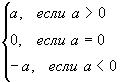 
Можно записать и так: | а | =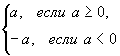 
Примеры: 
=
Противоположные числа имеют равные модули, т.е. 
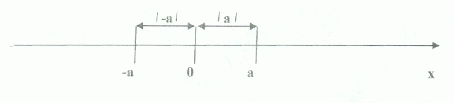
Расстояние от начала отсчета до точки, изображающей число, рассматривается всегда как величина неотрицательная.
Это можно считать геометрической интерпретацией модуля числа а.
Если | а | = 3, то а = 
3.
Уравнения и неравенства, содержащие модуль, решаются с использованием аналитического определения модуля, а так же и с использованием его геометрического смысла.
Уравнения вида | f(x)| = b, b
R
При b<0 решений нет,
При b=0 имеем f(x)=0,
При b>0 уравнение | f(x)| =b равносильно совокупности двух уравнений
Пример: | х-4| =3
откуда х = 7 и х = 1.
Второй способ. Пользуясь тем, что модуль разности двух чисел равен расстоянию между точками, изображающими эти числа, можно это уравнение решить так:
Прочитаем это соотношение так: расстояние от точки х до точки 4 равно 3. Откладываем на числовой прямой от точки 4 отрезок длиной 3 (в обе стороны)
Получим ответ: 7 и 1.
Уравнение вида f(| x| )=g(x), где f(x) и g(x) некоторые рациональные выражения
Уравнение равносильно совокупности систем: 
и 
Пример: решить уравнение х
+
-6=0
Данное уравнение равносильно совокупности систем:
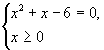и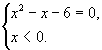 
Уравнение 
имеет два
решения: -3 и 2.
Решением уравнения 
являются числа 3 и –2.
Решением первой системы совокупности является неотрицательное число х=2.
Решением второй системы совокупности есть число –2.
Следовательно, решением данного уравнения являются два числа: 2 и –2.
Замечание:
Данное уравнение можно решать, используя метод замены неизвестного.
Пусть | х| =t, тогда 
и
уравнение можно записать так:
Решая его, находим корни. Это числа -3 и 2.
Берем только 2. Имеем | х| =2, т.е. х=
.
Уравнение вида | f(x)| =g(x)
Уравнение равносильно совокупности систем: 
и 
Пример: | 2х-5| =х-1
и 
и 
и 
Числа х=4 и х=2 удовлетворяют данному уравнению.
Второй способ. Уравнение | f(x)| =g(x) равносильно совокупности систем:
и 
Замечание: Если в уравнении | f(x)| =g(x) функция f(x) имеет более простой вид, чем g(x), то целесообразнее решать первым способом, а если более простой вид имеет функция g(x), то уравнение целесообразно решать вторым способом.
Уравнение вида | f1(x)| +| f2(x)| +…| fn(x)| =g(x)
Такие уравнения проще решать методом интервалов. Для этого находят сначала все точки, в которых хотя бы одна из функций | f1(x)| +| f2(x)| +…| fn(x)| меняет знак. Эти точки делят область допустимых значений уравнения на промежутки, на каждом из которых эти функции сохраняют знак. Затем, используя определение модуля, переходят от данного уравнения к совокупности систем, не содержащих знак модуля.
Пример: | 2х-3| +| х-3| =| 4х-1|
2х-3=0, х=1,5,
х-3=0, х=3,
4х-1=0, х=0,25
Вся числовая прямая разбивается на четыре промежутка.
На каждом промежутке решаем данное уравнение.
1) 
х = -5
2) 
х = 1
3)
Нет решений
4) 
Нет решений
Ответ: -5 и 1.
Пример: | | х-1| +2| =1
Можно при решении данного уравнения ввести вспомогательную переменную | х-1| = у. Тогда будем иметь простейшее уравнение | у+2| =1. Это уравнение решаем так:
Получаем: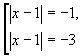 
Данные уравнения решения не имеют, т.к. модуль числа неотрицателен.
Ответ: решений нет.
Пример: | 2х+1| =4
Это уравнение можно решить, если свести его к решению совокупности двух систем.
Второй способ. Решить можно, исходя из геометрического смысла модуля.
| 2х+1| =4, | 2х-(-1)| =4, | 2(х-(-1/2))| =4,
2| (х-(-1/2))| =4, | х-(-1/2)| =2
Используем числовую прямую.
х
=-2,5, х
=1,5.
Пример: Решить систему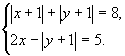 
Из второго уравнения выразим | у+1| и подставим в первое уравнение.
Получим систему: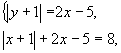 
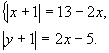
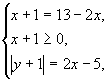
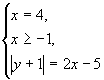
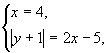
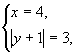
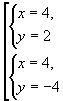
Ответ: (4; 2), (4; -4)
Решение неравенств, содержащих знак модуля
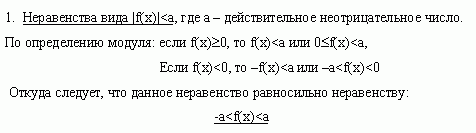
Примеры:
1) | 2х-5| <7
-7 < 2x-5 < 7
-2 < 2x < 12
-1 < x < 6
Ответ: (-1;6).
2) | x-3| >1
x-3 >1 и x-3 < -1
x > 4 и x < 2
Ответ: 
3. Неравенство вида f(| x| )<g(x), где f(x) и
g(x) – некоторые функции
Неравенство равносильно совокупности двух
систем:
и 
3) Решить неравенство:
Данное неравенство равносильно совокупности систем:
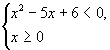и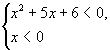 
); 
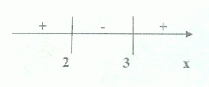
Решаем первую систему:
2<x<3
Решая вторую систему, получаем:
-3<x<-2
Ответ: 
Неравенство можно решать и при помощи замены переменной.
t = |x|, x2 = |x| = t2, t2 - 5t + 6 < 0 и т.д.
4. Неравенство вида | f(x)| <g(x), где f(x) и g(x) - некоторые функции
Данное неравенство равносильно системе: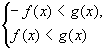
Для тех х, при которых, эта система,
(а значит и данное неравенство), решений не имеет.
4) Решить неравенство: 
Данное неравенство равносильно системе:
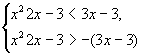
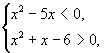
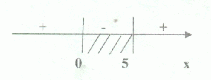
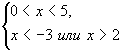2 < x < 5
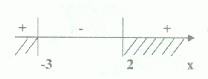
Ответ: (2; 5)
Второй способ: Неравенство равносильно совокупности двух систем
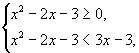
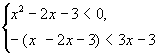
Решим первую систему: 
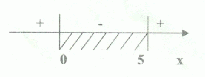
Решение первой системы: 
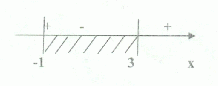
Решим вторую систему:
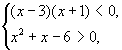
Решением этой системы является 2 < x < 3
Ответ: 
Третий способ: Находим точки, в которых функция y = x - 2x -3 меняет знак.
Отмечаем их на числовой прямой и решаем неравенство на каждом промежутке.
5. Решение неравенства вида | f(x)| >g(x)
Неравенство вида | f(x)| >g(x) , где f(x) и g(x)- выражения, зависящие от х, равносильно совокупности двух неравенств f(x)>g(x) и , f(x)<-g(x), т.е.
5) Решить неравенство
Находим точки, в которых хотя бы одна из функций
, 
меняет знак: х=1, х=5.
Отмечаем их на числовой прямой и рассмотрим
неравенство на каждом из трех промежутков: 
.
Заданное неравенство равносильно совокупности трех следующих систем неравенств:
Решение первой системы х<-1, вторая система не имеет решений и решение третьей системы х > 7
Ответ: 
6) Решить неравенство: | | 2х+1| -5| >2
Для упрощения решения введем новую переменную | 2х+у| =у
Будем иметь неравенство вида: | у-5| >2,
Тогда: у-5>2 и у-5<-2
y>7 и у<3
| 2х-1| <3 и | 2х+1| >7
Решаем неравенство: | 2х-1| <3
-3<2x+1<3
-4<2x<-2
-2<x<1
Решаем неравенство: | 2х+1| >7
2x+1>7 и 2x+1<-7
2x>6 и 2x<-8
x>3 и x<-4
Ответ: 
7) Решить неравенство: 
Неравенство равносильно совокупности двух систем:
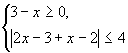
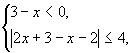
Решаем первую систему:
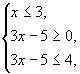или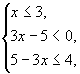 
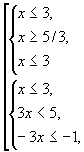
Решая вторую систему, получим: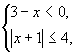 
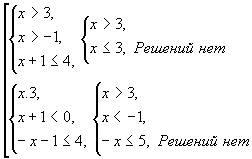
Ответ: 