Цели:
- Систематизировать знания по теме: “Решение различных типов тригонометрических уравнений”, обобщить и проверить уровень усвоение учебного материала.
- Развивать практические навыки при решении тригонометрических уравнений.
- Развивать представления о тригонометрических уравнениях как об уравнениях сводящихся к алгебраическим уравнениям, умение работать по заданному алгоритму.
- Воспитывать интерес к предмету, заинтересованность в ходе игры к данной теме, вызвать чувство ответственности за себя, организованности, дисциплины
“Счастливая случайность выпадает лишь на долю подготовленных умов” (Луи Пастернак)
План урока
- Оргмомент – 1 мин.
- Проверка домашнего задания – 3 мин. (проектор и кубик экзаменатор)
- Диктант – 5-7 мин.
- Дальше, дальше – 3 мин. ( маленькие листочки, переносные дощечки, электрифицированный стенд)
- Какая схема лишняя? – 3 мин.
- Спешите видеть!
а. Тест – 3 мин.
б. Динамические блоки – 4 мин.
в. Темная лошадка – 10 мин. - Конкурс капитанов -2 мин.
- Гонка за лидером (кроссворд) – 3 мин.
- “Заморочки” ( графический диктант) - 2 мин.
- Итог.
Тригонометрия – это чрезвычайно важный для жизни человека раздел математики. Сегодня у нас заключительный урок по теме “Тригонометрические уравнения”. Повторим, обобщим, приведем в систему методы решения уравнений, формулы, используемые для их решения.
Урок проводится в форме игры “Счастливый случай”, но не надо надеется на случай, так как “счастливая случайность выпадает лишь на долю подготовленных умов” -Л.Пастернак.
Первенство будут оспаривать четыре семьи. У каждой семьи свой капитан, который будет оценивать участие членов семьи, их вклад в общую победу.
Принято, что каждый день члены семьи начинают с зарядки, т.е. разминки.
I Гейм “Разминка”
Цель: Контроль (самоконтроль) знаний и приведение в систему знаний по решению простейших тригонометрических уравнений.
1 вариант
- Записать решения уравнения вида cos x=a при |a| > 1?
- При каком значении а, уравнение cos x =a имеет решения?
- Какой формулой выражается это решение?
- На какой оси откладывается значение а при решении уравнения cos x =a?
- Какому числовому промежутку принадлежат значения arccos a?
- Какому промежутку принадлежат значения а?
- Записать решения уравнения cos x =1.
- Записать решения уравнения cos x = -1.
- Записать решения уравнения cos x = 0.
- Найти arccos(-a).
- Какому промежутку принадлежат значения arctga?
- Какой формулой выражается решение уравнения tg x=a?
- Чему равен arctg (-a)?
2 вариант
- Записать решения уравнения вида sin x=a при |a| > 1?
- При каком значении а, уравнение sin x =a имеет решения?
- Какой формулой выражается это решение?
- На какой оси откладывается значение а при решении уравнения sin x =a?
- Какому числовому промежутку принадлежат значения arcsin a?
- Какому промежутку принадлежат значения а?
- Записать решения уравнения sin x =1.
- Записать решения уравнения sin x = -1.
- Записать решения уравнения sin x = 0.
- Найти arcsin(-a).
- Какому промежутку принадлежат значения arcctga?
- Какой формулой выражается решение уравнения ctg x=a?
- Чему равен arcctg (-a)?
Взаимопроверка выполненных заданий.
Учащиеся заносят результаты в лист учета

Нормы оценок: “5” - правильно выполнено 13 заданий;
“4” - правильно выполнено 10-12 заданий;
“3” - правильно выполнено 5-9 заданий;
“2” - правильно выполнено меньше 5 заданий.
II Гейм “Дальше, дальше…” (творческий)
Цель: Отработать понимание математической речи на слух, знание формул необходимых при решении уравнений.
1 человек от команды записывает ответы на переносных дощечках. 1 человек и капитан работают на электрифицированном стенде.
Всем:
1) Необходимо поставить в соответствие названию номер формулы и Вы получите шифр.
Формулы записаны на доске:
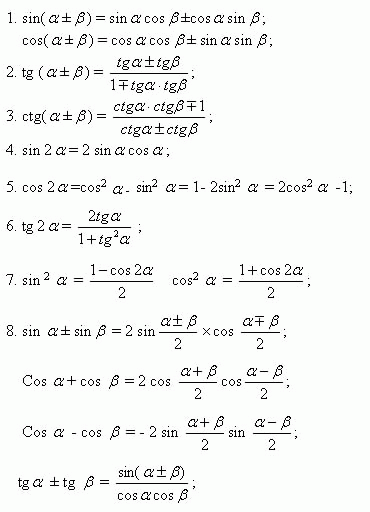
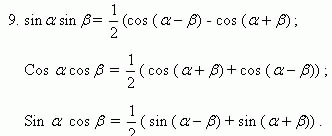
Под диктовку:
- Формула синуса двойного угла.
- Удвоенное произведение косинуса полусуммы на косинус полуразности;
- Формулы синуса и косинуса суммы и разности аргументов;
- Разность квадратов синуса и косинуса;
- Формулы понижения степени;
- Формулы тангенса суммы и разности аргументов;
- Формулы преобразования произведения тригонометрических функций в сумму.
Шифр: 4815729
Нормы оценок:
“5” +7
“4” + 5 – 6
“3” + 4 – 5
Оценки выставляются в лист учета.
2) Устные упражнения на определение вида простейших тригонометрических уравнений.
Слайд №1.
Ребята, здесь Вы видеть схемы решений тригонометрических уравнений.
Как Вы думаете, какая из схем этой группы лишняя?
Что объединяет остальные схемы?
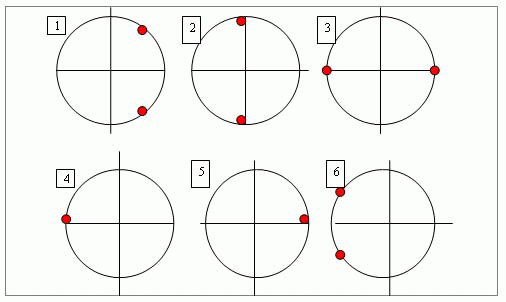
3 схема - лишняя, остальные решения уравнения cos x =a
Кто правильно ответил, то ставит + в лист учета.
Выслушивается по одному человеку от команды.
III Гейм “Спешите видеть, отвечать, решать”
1) Классификация тригонометрических уравнений.
Цель: привести в систему знания по типам и методам решения тригонометрических уравнений.Определить тип и метод решения уравнения.
Типы уравнений
- Уравнение, сводимые к алгебраическим.
- Однородные уравнения и приводимые к ним.
- Метод вспомогательного угла.
- Уравнения, решаемые разложением на множители.
- Уравнения, решаемые с помощью формул понижения степени.
- Частные приемы решения тригонометрических уравнений. (произведение, сумма, квадрат…)
- Универсальная подстановка.
Учащиеся сдают листочки на проверку.
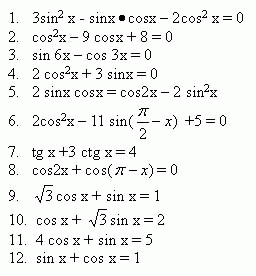
Методы решения:
- Однородное;
- Алгебраический;
- Разложение на множители;
- Алгебраический;
- Понижение степени, затем алгебраический;
- Алгебраический;
- Алгебраический;
- Алгебраический;
- Метод вспомогательного угла;
- Метод вспомогательного угла;
- Универсальная подстановка;
- Частные приемы.
Раунд “Отвечать”
Динамические блоки уравнений: на сравнение, обобщение и выделение главного, раскрытие идей решения некоторых уравнений, предупреждение возможной ошибки, выделение общего алгоритма решения тригонометрических уравнений.
1 команда: о чем идет речь?

1, 3, 4 – простейшие, решаются по известным формулам.
2- простейшее, с параметром, имеет решения при а=0
2 команда: о чем говорит этот блок уранений?
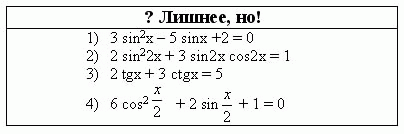
1, 3, 4 – одноименные, решаются методом подстановки, сводятся к алгебраическому.
2- однородное, но заменив sin2x + cos2x =1 и разделив на sin22x получим, решая методом подстановки сводим к алгебраическому.
3 команда: Что бы это значило?
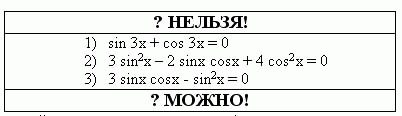
- – однородное уравнение 1 степени;
- - однородное уравнение 2 степени;
- – нельзя делить на sin2x – потеря корней! Можно вынести общий множитель или разделить на cos2x .
4 команда: найди лишнее и раскрой идею.
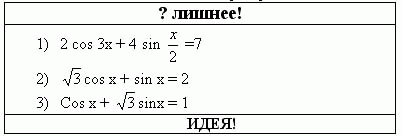
2, 3 – метод вспомогательного угла;
1 – решается оценкой левой и правой части.
Наибольшее значение левой части 6, а правой части
7. ![]() Нет решений.
Если правая часть 6, то необходимо решить систему
Нет решений.
Если правая часть 6, то необходимо решить систему
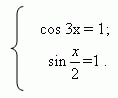
В это время, пока идет обсуждение идей по 1 человеку от команды выполняют тестовые задания на нахождение идей решения.
Цель: расширение математического кругозора.
При решении уравнений 1.1 – 1.4 выберите соответствующий из приемов 2.1- 2.4 и укажите нужную формулу или замену 3.1- 3.4

Ответы:
№ уравнения |
№ приема |
№ формулы |
1.1 |
2.3 |
3.4 |
1.2 |
2.1 |
3.3 |
1.3 |
2.4 |
3.2 |
1.4 |
2.2 |
3.1 |
Раунд “Решать”
“Темная лошадка”
Правильные ответы позволят узнать имена, исторические названия.
Дифференцированный тест. Каждый выбирает задания того уровня, который он выбрал. (В это время подводятся итоги)
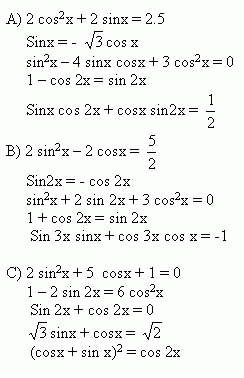
Одновременно от каждой команды по одному человеку работают у доски по карточкам.
Уровень А) в,а,б,в,б
ВИЕТ – Отец современной алгебры, любил разгадывать зашифрованные письма. Большой интерес к тригонометрии. Это было вызвано стремлением сделать астрономию более точной наукой. Буквы закрыты.
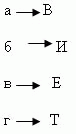
Уровень В) в,б,г,б,а
ФИНК – им введен термин “тангенс” ( от латинского “ tanger” - касаться.Это датский математик.
Уровень С) б,в,а,в,б
ДЖАЙБ – Своего рассвета тригонометрия достигла в странах Арабского Востока и Индии. В 4-5 веках индийский математик ввел термин для половины хорды. Ардха – половина, джива – выпуклость, а европейские с арабского на латынь – синус (синус – изгиб, кривизна).
IV Гейм “ Мозговая атака” (конкурс капитанов)
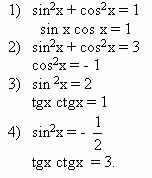
V Гейм “Гонка за лидером”
(Разгадать кроссворд, каждая команда получает кроссворд, по очереди разгадывают слова)
“ Мышление начинается с удивления” - заметил 2500 лет назад Аристотель.
Сухомлинский считал, “Что чувство удивления – могучий источник желания знать, от удивления к знаниям один шаг”. А математика – замечательный предмет для удивления.
VI Гейм “Заморочки”
Проходит в форме графического диктанта.

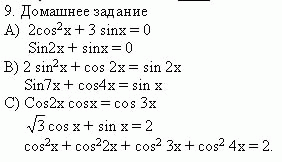
Приложение
Кроссворд
- Кофункция тангенса.
- От чего зависит значение функции.
- Мера измерения угла.
- Какой функции недостает: sinx, cosx, ctgx, …
- Значение тригонометрических функций повторяется через …
- у = cosx – тригонометрическая …
- Как называется график функции у = sinx?
- (0; ?) – что это?
- Он не только в земле, но и в математике.
- Предложение, требующее доказательства.
- Число из отрезка
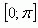 , косинус которого равен а.
, косинус которого равен а. - Отношение противолежащего катета к гипотенузе.
- у = sinx – нечетная функция, а у = cosx - …