Цели урока:
- Обучающая: познакомить учащихся с новыми понятиями: “координатная плоскость”, “система координат”, “прямоугольная система координат”, их использование в практических целях и в жизни человека, научить учащихся ориентироваться на координатной плоскости, находить координаты заданных точек, и по заданным координатам точки определять ее положение на координатной плоскости;
- Развивающая : развивать познавательную активность, творческие способности учащихся;
- Воспитательная : воспитание интереса к предмету с привлечением мультимедийных возможностей компьютера.
Оборудование:
- доска, мел,
- школьные принадлежности,
- наглядные пособия (плакаты),
- мультимедийные средства.
Ход урока
1. Организационный момент.
2. Устный счет (Приложение 1).

3. Опрос – введение в новую тему.

4. Объяснение нового материала.
– Общаясь друг с другом, люди часто говорят: "Оставьте свои координаты". Для чего?....Чтобы человека было легко найти. Это могут быть: номер телефона, домашний адрес, место работы, Е-mail. Главное здесь в том, что по этим данным человека можно будет найти.
Именно в этом и состоит суть координат или, как обычно говорят, системы координат: это правило, по которому определяется положение того или иного объекта.
Кроме почтовых адресов и номеров телефонов системы координат пронизывают всю практическую жизнь человека.
Кто из вас хотя бы раз не был в кинотеатре? Таких нет.

А кто из вас хоть раз не ездил на поезде? Таких тоже нет.

Более чем за 100 лет до н.э. греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами. Чтобы определить местонахождение объекта по карте нужно знать его координаты.
Также систему координат можно проследить при игре в шахматы и морской бой.
В игру “Морской бой” играют на 100-клеточной доске или на бумаге в клеточку, рисуя таблицу 10? 10. Каждая клетка на игровом поле определяется буквой и цифрой. Буквами помечены горизонтали игрового поля, а цифрами – вертикали.
Аналогичная система координат используется и в шахматах, только горизонтали на шахматной доске всегда обозначают латинскими буквами.

Такого рода “клеточные координаты” обычно используются на военных, морских, геологических картах. Применяются они и на туристических схемах городов для облегчения поиска нужной улицы или какой-либо достопримечательности.
Итак, вы уже, наверное, догадались, что для того, чтобы определить положение какой-либо точки на плоскости необходимо знать две ее координаты.
Возникает вопрос: “А как же все-таки определить положение точки на плоскости?”
Для этого на плоскости строят две перпендикулярные прямые (обычно одну из них располагают горизонтально, а другую – вертикально) и вводят на каждой из них обычные координаты. Эти координаты согласованны между собой. Точка пересечения прямых О называется началом координат. Эта буква выбрана не случайно, а по сходству написания с цифрой 0 или как первая буква латинского слова origo – начало. Сами координатные прямые называют осями координат.
Горизонтальную ось называют осью абсцисс (или осью Х), вертикальную ось называют осью ординат (или осьюY). Плоскость, на которой задана система координат, называется координатной плоскостью, которая разделяется осями абсцисс и ординат на четверти.
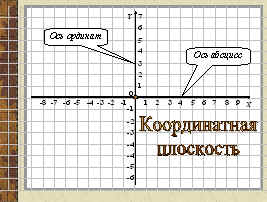
Посмотрим, как определяется положение точки на координатной плоскости.
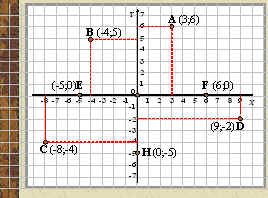
1. Устно решим задание из учебника № 1378, № 1379.
Посмотрим, как построить точки на координатной плоскости.
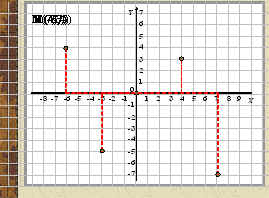
2. Решим на доске и в тетрадях № 1377, № 1381.
3. Обучающая самостоятельная работа.
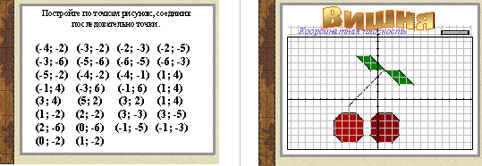
4. Демонстрация творческих работ учащихся прошлых лет.

