Цели:
- Развивать и укреплять интерес к математике, истории ее развития, мотивировать познавательную деятельность, развивать любознательность.
- Расширять математический кругозор учащихся.
- Прививать навыки самостоятельного поиска новых знаний.
- Содействовать развитию культуры коллективного труда.
Оборудование:
- портреты Архимеда, плакат со значением числа p , плакат с цитатами - “Эврика!”, “Дайте мне точку опоры, и я сдвину Землю!”, “Не трогай моих чертежей!”, “Бессмысленно воевать с геометрией”, рисунки метательных машин, чертежи многоугольников вписанных и описанных около окружности, спиралей, цилиндра и вписанного в него шара (примеры: <Рисунок1>, <Рисунок2>, <Рисунок3>, <Рисунок4>, <Рисунок5>, <Рисунок6>, <Рисунок7>, <Рисунок8>, <Рисунок9>);
- (ноутбук, проектор, цифровая доска, презентация) или (маркерная доска, маркер, губка).
Спектакль.
На сцене учащиеся что-то учат, бубнят (чередуется одновременное проговаривание всеми учениками и каждым в отдельности):
- Отношение длины окружности к диаметру…
- Сумма первых n-первых членов геометрической прогрессии …
- Сумма бесконечной геометрической прогрессии …
- Длина дуги …
- n-ный член арифметической прогрессии …
За отдельным столом первоклассник “колдует” над непонятным аппаратом. Внезапно загораются несколько лампочек, постепенно горящих лампочек становится больше. Слышится (отредактированная) песня из кинофильма “Иван Васильевич меняет профессию”:
Планета крутится круглая, круглая.
Летит планета вдаль сквозь суматоху дней.
Звенит январская вьюга, и ливни хлещут упруго,
И звезды мчатся по кругу, и шумят города …
Первоклассник:
- Ну что ж, придется повысить напряжение… Опасно? Но как говорится, риск дело … - загораются все лампочки, они начинают мигать. Внезапно загорается прожектор (включение прожектора совпадает со взрывом, записанным из кинофильма “Иван Васильевич меняет профессию”) и тот час же все выключается.
В это время на сцену выходят Архимед и горожанин. Учащиеся удивленно рассматривают незнакомцев. Архимед проходит по сцене, останавливается и начинает что-то чертить.
Горожанин:
- Эй, что ты там чертишь?
Архимед:
- Вычисляю. Знаете ли вы, что если найти точку опоры, можно перевернуть земной шар?
Горожанин:
- Перевернуть земной шар? Ого, в этой мыслишке что-то есть!
Учащиеся визжат.
Первоклассник:
- Ребята, выслушайте меня, только, умоляю вас, спокойно. Помните, я говорил вам о машине времени? Так вот сегодня мне этот опыт удался. Это - настоящий Архимед! – подходит к Архимеду и провожает его к креслу.
1 ученик:
- Да, да, это Архимед – древнегреческий ученый. Об Архимеде известно больше, чем о других ученых древности. Прежде всего, достоверен год его смерти – год падения Сиракуз, когда ученый погиб от руки римского солдата. До наших времен дошли сведения о чудесных изобретениях ученого. Известна история о золотом венце царя. Чистоту его состава Архимед проверил при помощи найденного им закона выталкивающей силы.
2 ученик:
Другая легенда рассказывает, что Архимед соорудил систему блоков, с помощью которой один человек мог спустить на воду огромный корабль “Сиракусия”. Крылатыми стали произнесенные тогда слова Архимеда: “Дайте мне точку опоры, и я поверну землю”. Инженерный гений Архимеда с особой силой проявился при осаде Сиракуз.
3 ученик:
До нас за очень много лет
В трудный год родные Сиракузы
Защищал ученый Архимед.
Многие орудья обороны
Были сконструированы им,
Долго бился город непреклонный,
Мудростью ученого храним.
Первоклассник:
- Воины римского консула Марцелла были надолго задержаны у стен города невиданными машинами: мощные катапульты прицельно стреляли каменными глыбами, в бойницах были установлены метательные машины, выбрасывающие грады ядер, береговые краны поворачивались за пределы стен и забрасывали корабли противника каменными и свинцовыми глыбами, крючья подхватывали корабли и бросали их вниз с большой высоты, системы вогнутых зеркал поджигали корабли. В “Истории Марцелла” Плутарх описывает ужас, царивший в рядах римских воинов: “Как только они замечали, что из-за крепостной стены показывается веревка или бревно, они обращались в бегство с криком, что вот Архимед еще выдумал новую машину на их погибель”.
Архимед (задумчиво):
- Огромен мой вклад и в развитие математики.
2 ученик:
- Теоретическими изысканиями в математике Архимед стал заниматься довольно поздно – в возрасте свыше 40 лет. Все его математические работы поражают сочетанием оригинальной мысли, мастерской техникой вычислений и строгостью доказательств. Обилие вычислений отличает его труды от творческих работ других греческих математиков, что сближает его с математиками Востока. Архимед развил методы нахождения площадей, поверхностей и объемов различных фигур и тел. Его математические работы намного опередили свое время и были правильно оценены только в эпоху создания дифференциального и интегрального исчисления.
Архимед:
- Много лет я посвятил исследованию различных линий, и особое место среди них занимали спирали. Спирали – плоские кривые линии, многократно обходящие одну из точек на плоскости, называемую полюсом спирали.
3 ученик:
- И впоследствии она была названа спиралью Архимеда. К ней он строил касательную и находил площадь ее витка. Геометрическим свойством, характеризующим спираль Архимеда, является постоянство расстояний между витками, каждое из них равно 2p a . По спирали Архимеда идет, например, звуковая дорожка. Перемещение острия корундовой иглы по этой дорожке будет результирующим двух равномерных движений: приближения к полюсу и вращения вокруг полюса. Металлическая пластинка с профилем в виде половины витка архимедовой спирали часто используется в конденсаторе переменной емкости. Одна из деталей швейной машины – механизм для равномерного наматывания ниток на шпульку – имеет форму спирали Архимеда.
4 ученик подходит к спирали, изображенной на фанерном диске, вращает диск и читает стихотворение “Спираль Архимеда”:
Для того, чтоб все значенье Архимедовой спирали,
Кривизну и измеренье мы доподлинно узнали,
Соберемся тесным кругом, сговоримся все друг с другом,
И споем мы хоровую про спиральную кривую.
Диск вокруг себя вращаем, темп все больше ускоряем,
Все скорее, все быстрее,
К центру шибко, бойко, гибко!
Вот так встряска! Словно пляска!
Эй, галоп!.. Центр – стоп.
При вращении диска в одном направлении спираль закручивается, при вращении в другом – раскручивается. Спираль словно оживает.
Архимед задумчиво:
- Я вычислил с большой точностью отношение длины окружности к ее диаметру.
5 ученик (выполняя записи на доске):
- Вопрос о вычислении отношения длины окружности
к своему диаметру, т.е. числа p , занимал лучшие умы
человечества на протяжении тысячелетий, а первое
вычисление p на основе строгих теоретических
рассуждений было предпринято Архимедом. В своем
произведении “Измерение круга”, желая выразить
отношение длины окружности к своему диаметру, он
заключил окружность между вписанным и описанным
около нее шестиугольниками, затем, удваивая
число сторон этих многоугольников, сближал их с
окружностью. Для нахождения длины сторон
избранного им описанного шестиугольника он взял
приближенное значение
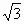 . В тексте работы совершенно без
пояснения он берет значение этого корня, которое
в современной записи выглядит так:
. В тексте работы совершенно без
пояснения он берет значение этого корня, которое
в современной записи выглядит так: 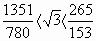 . Используя взятое значение
корня из трех, Архимед определяет через радиус
длину стороны правильного шестиугольника
(описанного, а также и вписанного). Затем,
последовательно удваивая число сторон, находит
длины сторон двенадцатиугольников, дальше –
длины сторон многоугольников с 24, 48 и, наконец, 96
углами. В результате он получил следующее
выражение:
. Используя взятое значение
корня из трех, Архимед определяет через радиус
длину стороны правильного шестиугольника
(описанного, а также и вписанного). Затем,
последовательно удваивая число сторон, находит
длины сторон двенадцатиугольников, дальше –
длины сторон многоугольников с 24, 48 и, наконец, 96
углами. В результате он получил следующее
выражение: 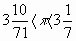 .
Арифметическое среднее значение верхней и
нижней границ дает
.
Арифметическое среднее значение верхней и
нижней границ дает 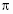
 3,1419.
3,1419.
1 ученик:
- Истинное значение этого числа 3,14159…, т.е.
неточность, какая получилась в расчетах
Архимеда, допущена лишь в четвертом десятичном
знаке. Выведенное Архимедом для
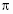 приближенное значение
приближенное значение 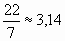
оказалось вполне удовлетворительным для практики. На это значение ссылаются Герон Александрийский, Папп, Прокл и другие ученые. Оно широко применяется и в настоящее время. Созданный Архимедом метод вычисления длины окружности посредством периметров вписанных и описанных многоугольников применялся многими видными математиками на протяжении почти 2000 лет.
2 ученик:
- Вычисление большого числа знаков для ![]() не имеет
практического значения, однако многие ученые
стараются найти для
не имеет
практического значения, однако многие ученые
стараются найти для ![]() значение, превосходящие по точности
ранее известные. В своей книге “Об измерении
окружности” (1424) ал-Каши, рассмотрев вписанный и
описанный многоугольники с 800 335 168 сторонами,
получает в результате для p 16 верных десятичных
знаков. В 1597 г. А. Ван Ромен из Лувена (Бельгия),
применяя метод Архимеда с помощью 230-угольников,
получил 17 верных десятичных знаков. Большое
терпение и выдержку обнаружил голландский
вычислитель Лудольф ван-Цейлен (1540-1610), который
применяя метод Архимеда, дошел до
многоугольников с 60·2029 степени сторонами,
получив 35 верных десятичных знаков для p . В его
честь число
значение, превосходящие по точности
ранее известные. В своей книге “Об измерении
окружности” (1424) ал-Каши, рассмотрев вписанный и
описанный многоугольники с 800 335 168 сторонами,
получает в результате для p 16 верных десятичных
знаков. В 1597 г. А. Ван Ромен из Лувена (Бельгия),
применяя метод Архимеда с помощью 230-угольников,
получил 17 верных десятичных знаков. Большое
терпение и выдержку обнаружил голландский
вычислитель Лудольф ван-Цейлен (1540-1610), который
применяя метод Архимеда, дошел до
многоугольников с 60·2029 степени сторонами,
получив 35 верных десятичных знаков для p . В его
честь число ![]() было названо современниками “Лудольфово
число”, на его надгробном камне было высечено
найденное им значение
было названо современниками “Лудольфово
число”, на его надгробном камне было высечено
найденное им значение ![]() .
.
3 ученик:
- Начиная с конца XVII в. для вычисления ![]() применяются
более эффективные методы высшей математики.
Леонард Эйлер вычислил
применяются
более эффективные методы высшей математики.
Леонард Эйлер вычислил ![]() с точностью до 153 верных десятичных
знаков. После опубликования его работы (1736) стало
общепринятым обозначение
с точностью до 153 верных десятичных
знаков. После опубликования его работы (1736) стало
общепринятым обозначение ![]() (первая буква в греческом слове
“периферия” - круг), которое встречается впервые
в 1706 г. у английского математика У. Джонса. В 1873 г.
англичанин В. Шенкс определил p с точностью до 707
десятичных знаков, усердно проработав для этой
цели целых 15 лет. Однако, как выяснилось
впоследствии, 527-й знак Шенкса оказался неверным.
Ошибка была обнаружена Фергюссоном и Ренчем,
которые в 1948 г. получили значение
(первая буква в греческом слове
“периферия” - круг), которое встречается впервые
в 1706 г. у английского математика У. Джонса. В 1873 г.
англичанин В. Шенкс определил p с точностью до 707
десятичных знаков, усердно проработав для этой
цели целых 15 лет. Однако, как выяснилось
впоследствии, 527-й знак Шенкса оказался неверным.
Ошибка была обнаружена Фергюссоном и Ренчем,
которые в 1948 г. получили значение ![]() с 808 знаками. С помощью электронных
машин в 1949 г. получено значение
с 808 знаками. С помощью электронных
машин в 1949 г. получено значение ![]() с 2035 знаками, а позднее – с 3089
знаками всего лишь за 13 с. К 1963 г. было найдено уже
100265 десятичных знаков числа
с 2035 знаками, а позднее – с 3089
знаками всего лишь за 13 с. К 1963 г. было найдено уже
100265 десятичных знаков числа ![]() .
.
4 ученик (подходя к плакату со
значением числа ![]() ):
):
- В настоящее время с помощью ЭВМ число “пи” вычислено с точностью более пятисот тысяч знаков, причем эти вычисления продолжались только несколько часов. Вычисление такого большого числа знаков для p не имеет практического значения, а показывает лишь огромное преимущество и совершенство современных средств и методов вычисления по сравнению со старыми.
3,1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104…
Архимед продолжает:
- Я вычислял площадь круга…
5 ученик:
- Вначале Архимед вписывал в круг шестиугольник, затем на каждой стороне построил равнобедренный треугольник – получался двенадцатиугольник. Постепенно удваивая число сторон, Архимед получил 24-угольник, 48-угольник и, наконец, 96-угольник. Построенные многоугольники все более и более покрывали собой площадь круга, как бы постепенно “исчерпывая” ее. Между прочим, этот метод нахождения площади круга до сих пор, через 2200 лет после смерти Архимеда, излагается в современных школьных учебниках геометрии.
Архимед:
- В ходе своих исследований нашел сумму бесконечной геометрической прогрессии со знаменателем 1/4, что явилось первым примером появления в математике бесконечного ряда…
1 ученик, быстро записывает на доске маркером (либо подготовленная презентация и записи на интерактивной доске):
- Еще в V в. до н.э. греки знали следующие прогрессии и их суммы:
- 1+2+3+…+n=
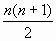 ;
; - 2+4+6+…+2n=n(n+1);
- 1+3+6+…+(2n+1)=(n+1)2 и др.
В “Исчислении песчинок” Архимед впервые сопоставляет арифметическую и геометрическую прогрессии:
1, 2, 3, 4, 5, …
10, 102, 103, 104, 105, …
и указывает на связь между ними, например:
103? 105=103+5=108,
т.е. для умножения двух членов геометрической прогрессии достаточно сложить соответствующие члены арифметической прогрессии и взять полученную сумму в качестве показателя 10.
2 ученик, продолжая запись:
Одно из доказательств Архимеда, изложенное в его произведении “Квадратура параболы”, сводится к суммированию бесконечно убывающей геометрической прогрессии:
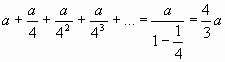 .
.
3 ученик, продолжая запись:
Для решения некоторых задач из геометрии и механики Архимед вывел формулу суммы квадратов натуральных чисел, хотя ею пользовались и до него:
![]() .
.
4 ученик:
В “Науке о числах” (1484) Н. Шюке, как и Архимед, сопоставляет арифметическую прогрессию с геометрической и дает общее правило для суммирования любой бесконечно убывающей геометрической прогрессии.
Архимед:
- Потомки! Во многом вы преуспели, - и с грустью продолжает – мой вклад в математику был бы гораздо больше, но…
5 ученик:
- Много месяцев римляне стояли у стен Сиракуз и так бы не взяли город, если бы не праздник богини Артемиды, который осажденные отметили слишком усердно. Ночью штурмовой отряд римлян бесшумно поднялся на стены, перебил уснувшую стражу и ворвался в город. Озлобленные солдаты крушили и жгли все подряд. Говорят, даже Марцелл плакал, видя, как гибнет красивейший город, но остановить свои разъяренные войска он не мог. Он только просил не трогать Архимеда, у которого хотел узнать тайну его необычных машин. Но …
1 ученик:
Законы воинского счастья
До сих пор никем не учтены,
И втекают вражеские части
В темные пробоины стены.
Замыслом неведомым охвачен,
Он не знал, что в городе враги,
Он чертил задумчивый, не гордый,
Позабыв текущие дела, -
И внезапно непонятной хордой
Тень копья чертеж пересекла.
Появляются римляне и направляются к Архимеду. Навстречу воинам идет горожанин:
- Не троньте, не троньте его кругов!
2 ученик: - Один из пришлых римлян врагов с ученым вступает в беседу:
- Что толку в расчетах твоих, старик? – легат вопрошает с улыбкой. - Ты строишь расчеты свои на песке, на почве особенно зыбкой!
3 ученик:
Но убийц спокойствием пугая,
Он, не унижаясь, не дрожа,
Руку протянул, оберегая
Не себя, а знаки чертежа.
Архимед:
- Солдат, Вы меня извините, но мудрость жива и в сыпучих песках, а глупость мертва и в граните.
Римлянин поднимает копье.
4 ученик:
Он в глаза солдатам глянул смело.
Архимед:
Убивайте, римляне – враги!
Убивайте раз такое дело,
Но не наступайте на круги!
Римлянин:
- Старик, я вижу, ты - мастер красивых слов,
4 ученик:
- сказал и убил Архимеда.
Архимед падает. В это время загораются лампочки на “машине времени”, звучит музыка. Часть сцены, где остался Архимед, закрывается занавесом. Постепенно гаснут лампочки.
5 ученик:
- Солдату и в голову не пришло, что перед ним сам Архимед, и он убил ученого.
1 ученик:
Прошла столетий вереница,
Научный подвиг не забыт,
Никто не знает, кто убийца,
Но знают все, кто был убит…
2 ученик:
- В IXI-X веках работы Архимеда переводились на арабский язык, с XIII века они появляются в Западной Европе в латинском переводе. С XVI века начинают выходить печатные издания Архимеда, в XVII-XIX веках они переводятся на новые языки. Первое издание трудов Архимеда на русском языке относится к 1823 году.
3 ученик:
- Центральной темой математических работ Архимеда являются задачи на нахождение площадей поверхностей и объемов. Решение многих задач этого типа Архимед первоначально нашел, применяя механические соображения, по существу сводящиеся к методу неделимых, а затем строго доказал методом исчерпывания, который он значительно развил. Архимед вычислил площадь эллипса, параболического сегмента, нашел площадь поверхности конуса и шара, объем шара и сферического сегмента, а также объемы различных тел вращения и их сегментов.
4 ученик:
- Архимед нашел, что объемы цилиндра и вписанного в него шара относятся как 3 к 2. Этот результат ученый считал настолько важным, что завещал отобразить его на своей могильной плите.
5 ученик:
Спустя почти две сотни лет знаменитый римский оратор Цицерон стал управителем острова Сицилия. Прогуливаясь по заброшенной местности, он нашел среди кустарников надгробие с изображением шара, вписанного в цилиндр. Это была могила Архимеда. Сограждане похоронили его так, как он просил. О могиле потом забыли.
1 ученик:
Но законы геометрии и физики, открытые им, навсегда остались в науке, как осталась в истории и слава мужественного защитника города.
Литература.
- Математический энциклопедический словарь, гл. редактор Ю.В. Прохоров, Москва, “Советская энциклопедия”, 1988 г.
- Школьная энциклопедия МАТЕМАТИКА, гл. редактор С.М. Никольский, Москва, Научное издательство “Большая Российская Энциклопедия”, 1996 г.
- Г.И. Глейзер “История математики в школе VII-VIII класс”, Москва, “Просвещение”, 1982 г.
- Энциклопедия школьника “Всемирная история в лицах. Древний мир”, Москва, “Олма-Пресс”, 1999г.
- Журналы “Математика в школе”, 1995 г.