Пояснительная записка
Текстовые задачи представляют собой раздел математики, традиционно предлагаемый на государственной аттестации по математике. Они вызывают трудности у многих учащихся. Отчасти это происходит от недостаточного внимания, уделяемого такого сорта задачам в школьном курсе математике. В этом элективном курсе попытаемся восполнить данный пробел.
Задачи, предлагаемые в данном курсе, интересны и часто не просты в решении, что позволяет повысить учебную мотивацию учащихся и проверить свои способности к математике. Вместе с тем содержание курса позволяет ученику любого уровня активно включаться в учебно-познавательный процесс и максимально проявить себя: занятия могут проводиться на высоком уровне сложности, но включать в себя вопросы, доступные и интересные всем учащимся.
Цели:
- расширить знания учащихся о методах и способах решения текстовых задач;
- решение уравнений, неравенств и их систем;
- создать базу для развития способностей учащихся;
- помочь учащимся оценить возможности овладения курсом с точки зрения дальнейшей перспективы;
- предоставить учащимся возможность реализовать свой интерес к выбранному предмету;
- уточнить готовность и способность ученика осваивать выбранный предмет на повышенном уровне.
Задачи:
- познакомить учащихся со стандартными и нестандартными способами решения текстовых задач;
- научить преобразовывать выражения, возникающие при решении уравнении и неравенств;
- развивать логическое мышление и способности учащихся к математической деятельности;
- предоставить учащимся возможность проанализировать свои способности к математической деятельности.
Место курса в системе предпрофильной подготовки: курс ориентирован на предпрофильную подготовку учащихся по математике. Он расширяет базовый уровень по математике, является предметно ориентированным, способствует совершенствованию и развитию важнейших математических знаний и умений, предусмотренных школьной программой, поможет оценить свои возможности по математике и более осознанно выбрать профиль дальнейшего обучения.
Содержание программы
Тема 1. Задачи на числовые зависимости
(2ч).
Тема 2. Задачи на проценты (2ч).
Тема 3. Задачи на смеси и сплавы (2ч).
Тема 4. Задачи на движение (2ч).
Тема 5. Задачи на совместную работу (2ч).
Тема 6. Задачи на прогрессии (2ч).
Тема 7. Задачи практического применения
с геометрическим содержанием (2ч).
Тема 8. Как можно обойтись без уравнений
(1ч).
Итоговое занятие по защите проектов учащихся.
См. Приложение 1 (Учебно-тематический план)
Тема 1. Задачи на числовые зависимости
Теоретическая часть. При решении задач на числовые зависимости могут оказаться полезными следующие сведения:
1. Если натуральное число А имеет n знаков, то ![]() соответственно цифры единиц, десятков, сотен,… в
числе А.
соответственно цифры единиц, десятков, сотен,… в
числе А.
2.Если при делении натурального числа А на натуральное число В в частном получается q, а в остатке r (r <В), то А=Вq+r.
Пример 1. Найдите двузначное число, если известно, что количество единиц в нем на 2 больше, чем десятков, и произведение искомого числа на сумму его цифр равно 144.
Решение. Пусть в искомом числе содержится х
единиц. Тогда в нем (х–2)десятков, и,
следовательно , оно равно (х–2)10+х=11х–20.
Сумма цифр искомого числа равна (х–2)+х=2х–2.
Таким образом, получаем уравнение (11х–20)(2х-2)=144.
это уравнение имеет два корня: ![]() Из найденных значений х
этим условиям удовлетворяет только значение х=4.
Из найденных значений х
этим условиям удовлетворяет только значение х=4.
Пример 2. Найти два двузначных числа , о которых известно следующее: если к первому числу приписать справа второе число, а затем еще цифру 0, то получится пятизначное число, дающее при делении на квадрат второго числа в частном 39,а в остатке 575: если же к первому числу приписать справа второе и затем из составленного таким образом числа вычесть другое число, полученное приписыванием справа первого числа ко второму, то разность будет равна 1287.
Решение. Пусть х – первое число и у –
второе. После приписывания справа числа у к числу
х получится четырехзначное число ![]() , а после приписывания к
этому числу справа цифры 0 получится
, а после приписывания к
этому числу справа цифры 0 получится ![]() , при делении
этого числа на число
, при делении
этого числа на число ![]() в частном получается 39 и в остатке 575,
то
в частном получается 39 и в остатке 575,
то ![]() . Это
первое уравнение составляемой системы
уравнений. После приписывания справа
двузначного числа х к двузначному числу у
получится четырехзначное число
. Это
первое уравнение составляемой системы
уравнений. После приписывания справа
двузначного числа х к двузначному числу у
получится четырехзначное число ![]() , получаем второе
уравнение:
, получаем второе
уравнение: ![]() .
Итак, приходим к системе уравнений
.
Итак, приходим к системе уравнений
![]()
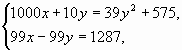
которая имеет два решения: (48;35) и ![]() . По смыслу задачи x и y
– натуральные числа, причем 10
. По смыслу задачи x и y
– натуральные числа, причем 10![]() x
x![]() 99 и 10
99 и 10![]() y
y![]() 99,
т.е. искомыми являются числа 48 и 35.
99,
т.е. искомыми являются числа 48 и 35.
Практическая часть
Задача 1. Сумма квадратов цифр двузначного числа равна 10. Если от искомого числа отнять 18, получится число, записанное теми же цифрами, но в обратном порядке. Найдите исходное число. (Ответ: 31)
Задача 2. Какое двузначное число в 4 раза больше суммы своих цифр и в 3 раза больше произведения цифр? (Ответ: 24)
Задача 3. Сумму всех четных двузначных чисел разделили без остатка на одно из них. Найдите делитель, если известно, что сумма его цифр равна 9 и что частное отличается от делителя только порядком цифр. (Ответ: 54)
Задача 4. Если двузначное число разделить на сумму его цифр, то в частном получится 7 и в остатке 6. Если же двузначное число разделить на произведение его цифр, то в частном получится 3, а в остатке число, равное сумме цифр исходного числа. Найдите исходное число. (Ответ: 83)
Тема 2. Задачи на проценты
Теоретическая часть включает определение
процента, нахождение процентов данного числа,
нахождение числа по его процентам, нахождение
процентного отношения чисел, формулу сложных
процентов: Аn = A0 ![]() , где А0 – начальный
момент времени, p – процентный прирост в
единицу времени, n – количество этих этапов.
, где А0 – начальный
момент времени, p – процентный прирост в
единицу времени, n – количество этих этапов.
Пример 1. Цена товара ежемесячно уменьшалась на одно т тоже число процентов от предыдущей цены. Определить на сколько процентов от предыдущей цены уменьшается цена товара, если выставленный на продажу телевизор за 8000р после двух снижений продан за 5120р.
А n= 5120, А 0 = 8000, n = 2. Найти p.
5120=8000 ·
; p = 20%
Ответ: 20%.
Пример 2. Цену товара сначала снизили на 20%, а затем новую цену ещё на 15% и затем ещё на 10%. На сколько процентов всего снизили первоначальную цену товара?
А 0 = 1.
А 3= 1
;
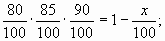
Ответ: 38,8%.
Практическая часть
Задача 1. В библиотеке имеются книги на английском, французском и немецком языках. Английские составляют 36% всех книг, французские – 75% английских, а остальные 185 книг – немецкие. Сколько книг на иностранных языках в библиотеке? (Ответ: 500 книг.)
Задача 2. Свежие грибы содержат по массе 90% воды, а сухие 12%. Сколько сухих грибов получится из 22кг свежих? (Ответ: 2,5 кг.)
Задача 3. Каково минимально возможное число учеников в выпускном классе школы, если известно, что процент неуспевающих в классе заключён в пределах от 2,5% до 2,9%? (Ответ: 35)
Задача 4. Цену товара снизили на 30%, затем новую цену повысили на 30%. Как изменилась цена товара? (Ответ: 91%)
Задача 5. Вкладчик положил в банк 62500р. Какая сумма окажется на счёте через 3 года, если банк выплачивает 4% годовых? (Ответ: 70304р.)
Тема 3. Задачи на сплавы и смеси
Теоретическая часть. Если смесь (сплав,
раствор) массы m состоит из вещества А,В,С (которые
имеют массы соответственно ![]() ), то величину
), то величину ![]() (соответственно
(соответственно ![]() ) называют концентрацией
вещества А (соответственно В, С) в смеси.
Величину
) называют концентрацией
вещества А (соответственно В, С) в смеси.
Величину ![]() (соответственно
(соответственно ![]() ) называют процентным содержанием
вещества А (соответственно В, С) в смеси.
) называют процентным содержанием
вещества А (соответственно В, С) в смеси. ![]() , т.е. от
концентрации двух веществ зависит концентрации
третьего.
, т.е. от
концентрации двух веществ зависит концентрации
третьего.
При составлении уравнения прослеживают содержание какого-нибудь одного вещества.
Пример. Имеется кусок сплава меди с оловом массой 12 кг, содержащий 45% меди. Сколько чистого олова надо прибавить к сплаву, чтобы получившийся новый сплав содержал 40% меди?
Решение. Сплав состоит из меди и олова. Проследим за содержанием олова в сплаве.
В 12 кг сплава было 45% меди, а олова в нем было 55%,
т.е. ![]() кг олова.
Пусть к первоначальному сплаву добавили x кг
олова. Тогда получилось (12 + x) кг нового сплава, в
котором олова стало 60%, т.е.
кг олова.
Пусть к первоначальному сплаву добавили x кг
олова. Тогда получилось (12 + x) кг нового сплава, в
котором олова стало 60%, т.е. ![]() кг.
кг. ![]()
Решив его, найдем x = 1,5. По смыслу задачи x > 0. Следует добавить 1,5 кг олова.
Практическая часть
Задача 1. Имеется сталь двух сортов с содержанием никеля 5% и 40%.Сколько стали одного и другого сорта взять, чтобы после переплавки получить 140 т стали с содержанием никеля 30%? (Ответ: 40 т и 100 т)
Задача 2. При смешивании 40% раствора кислоты с 10% раствором кислоты получили 800 г 21,25% раствора. Сколько граммов каждого раствора было для этого взято? (Ответ: 300 г и 500 г)
Задача 3. Свежие огурцы, содержащие 98% воды, имели массу 100 кг. Когда огурцы немного усохли, в них стало 96% воды. Какова стала масса огурцов после усыхания? (Ответ: 50 кг)
Задача 4. Из 40 т руды выплавляют 20 т металла, содержащего 6% примесей. Каков процент примесей в руде? (Ответ: 53%)
Тема 4. Задачи на движение
Теоретическая часть. Движение
характеризуется тремя компонентами: пройденный
путь, скорость и время. Путь = скорость ![]() время. Если тело с собственной
скоростью x движется по реке, скорость
течения которой равна y, то скорость тела по
течению считают равной (x + y), а против
течения – равной (x – y).
время. Если тело с собственной
скоростью x движется по реке, скорость
течения которой равна y, то скорость тела по
течению считают равной (x + y), а против
течения – равной (x – y).
Пример 1. Из пункта А в В выехал грузовой автомобиль, через 1 ч из А и В – легковой автомобиль. В пункт В автомобили прибыли одновременно. Если бы из пунктов А и В машины выехали одновременно навстречу друг другу, то встреча произошла бы через 1 ч 12 мин после выезда. За какое время проедет расстояние от А до В грузовик?
Решение. Пусть грузовик проезжает
расстояние от А до В за x ч. Тогда
легковой автомобиль проедет это расстояние за (x
– 1) ч. Полагая расстояние АВ равным y км,
найдем, что скорость грузового автомобиля равна ![]() км/ч, а
легкового равна
км/ч, а
легкового равна ![]() км/ч. Так как автомобили при движении
навстречу сближаются со скоростью
км/ч. Так как автомобили при движении
навстречу сближаются со скоростью ![]() км/ч, а весь путь они
проезжают за
км/ч, а весь путь они
проезжают за ![]() ч, получаем уравнение
ч, получаем уравнение ![]() После деления обеих частей уравнения
на
После деления обеих частей уравнения
на ![]() получим
уравнение
получим
уравнение ![]() содержащее только искомую неизвестную величину
x. Решив это уравнение, находим
содержащее только искомую неизвестную величину
x. Решив это уравнение, находим ![]()
По смыслу задачи x > 1. Ясно, что грузовик
проедет расстояние АВ за время, большее чем ![]() ч, т.е. x >
ч, т.е. x > ![]() . Этому условию
удовлетворяет только x = 3. Ответ:3ч.
. Этому условию
удовлетворяет только x = 3. Ответ:3ч.
Практическая часть
Задача 1. Пассажир, сидящий в поезде, который идет со скоростью 40 км/ч, заметил, что мимо окна в противоположном направлении в течение 3 с прошел встречный поезд, длина которого 75 м. Какова скорость встречного поезда? (Ответ: 50 км/ч)
Задача 2. Катер прошел против течения реки 8 км, повернул обратно и прошел по течению 36 км. Весь рейс продолжался 2 ч. Затем катер прошел против течения реки 6 км и по течению 33 км, затратив на этот второй рейс 1 ч 45 мин. Найдите скорость катера в стоячей воде. (Ответ: 20 км/ч)
Задача 3. Два велосипедиста выехали одновременно из пунктов А и В навстречу друг другу. Велосипедист из А, прибыл в В через 4 ч после встречи, а велосипедист из В, прибыл в А через 9 ч после встречи. Сколько часов был в пути каждый велосипедист? (Ответ: 15 ч и 10 ч)
Задача 4. На путь из А и В теплоход затрачивает 3 ч, на обратный путь – 4 ч. Сколько времени будет плыть плот из А в В? (Ответ: 24 ч)
Тема 5. Задачи на совместную работу
Теоретическая часть. Содержание задач этого типа сводится обычно к следующему. Некоторую работу, объем которой не указывается и не является искомым, выполняют несколько человек или механизмов, работающих равномерно. Объем всей работы, которая должна быть выполнена, принимается за единицу. Время t, требующееся для выполнения всей работы, и V – производительность труда, т.е. величина работы, выполняемой за единицу времени, связаны соотношение
![]() .
.
Пример. Первому трактору на вспашку всего поля требуется на 2 ч меньше, чем третьему трактору, и на 1 ч больше, чем второму. При совместной работе первого и второго тракторов поле может быть вспахано за 1 ч 12 мин. Какое время на вспашку поля будет затрачено при совместной работе всех трех тракторов?
Решение. Примем величину работы (в данном
случае это вспашка всего поля) за единицу. Пусть x
ч – время, необходимое для вспашки поля первому
трактору, y ч – второму и z ч – третьему.
Тогда ![]() –
производительность первого трактора,
–
производительность первого трактора, ![]() – второго и
– второго и ![]() – третьего. По
условию z – x = 2 и x – y = 1. Так как при
совместной работе первого и второго тракторов
выполняется
– третьего. По
условию z – x = 2 и x – y = 1. Так как при
совместной работе первого и второго тракторов
выполняется ![]() часть работы в час, а вся работа выполняется ими
за 1 ч 12 мин, т.е. за
часть работы в час, а вся работа выполняется ими
за 1 ч 12 мин, т.е. за ![]() ч, то
ч, то ![]() .
.
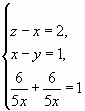
Решив, получим (3; 2; 5), (-0,4; -0,6; 2,4). По смыслу задачи
x > 1, y > 0 и z > 2. Из найденных
решений этим условиям удовлетворяет только
первое решение. При совместной работе трех
тракторов производительность составит ![]() , т.е.
, т.е. ![]() . На вспашку
поля тремя тракторами затрачено
. На вспашку
поля тремя тракторами затрачено ![]() ч.
ч.
Практическая часть
Задача 1. На двух копировальных машинах, работающих одновременно, можно сделать копию пакета документов за 10 мин. За какое время можно выполнить эту работу на каждой машине в отдельности, если известно, что на первой машине ее можно сделать на 15 мин быстрее, чем на второй? (Ответ: 15 мин и 30 мин)
Задача 2. Два строителя выложили стену из кирпичей за 14 дней, причем второй присоединился к первому через 3 дня после начала работы. Известно, что первому строителю на выполнение всей работы потребовалось бы на 6 дней больше, чем второму. За сколько дней мог бы выложить эту стену каждый строитель, работая отдельно? (Ответ: За 28 дней и за 22 дня)
Задача 3. Две снегоуборочные машины, работая вместе, могут очистить определенную территорию от снега за 4 ч. Если бы сначала первая машина выполнила половину работы, а затем ее сменила вторая, то на всю уборку снега ушло бы 9 ч. За какое время может очистить от снега эту территорию каждая машина в отдельности? (Ответ: Одна машина за 6 ч, другая – за 12 ч.)
Задача 4. Два оператора, работая вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй – 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно? (Ответ: первый за 12 ч, второй – за 24 ч)
Тема 6. Задачи на прогрессии
Теоретическая часть. Даются определения арифметической и геометрической прогрессий, их свойства.
Пример. Найдем трехзначное число, цифры которого образуют арифметическую прогрессию и которое делится на 45.
Решение. Пусть x –сотни, y –десятки и z
– единицы искомого числа. Так как числа x, y, z
образуют арифметическую прогрессию, то ![]() . Искомое число
делится на 45, то оно делится и на 5, и на 9. Значит,
оно оканчивается либо цифрой 0, либо цифрой 5 и
сумма его цифр делится на 9. Таким образом,
возникают две возможности, и в соответствии с
этим мы приходим к совокупности двух систем
уравнений (отличающихся только первым
уравнением):
. Искомое число
делится на 45, то оно делится и на 5, и на 9. Значит,
оно оканчивается либо цифрой 0, либо цифрой 5 и
сумма его цифр делится на 9. Таким образом,
возникают две возможности, и в соответствии с
этим мы приходим к совокупности двух систем
уравнений (отличающихся только первым
уравнением):
где
. Из первой системы следует, что
Перебрав натуральные значения y от 1 до 9,
убеждаемся, что этой системе удовлетворяют лишь
пары (6; 3), (12; 6), (18;9). Однако по смыслу задачи x и y
– натуральные числа, удовлетворяющие
неравенствам ![]() и
и ![]() . Этим
условиям удовлетворяет только пара (6; 3).
. Этим
условиям удовлетворяет только пара (6; 3).
Из второй системы следует, что
Аналогично, перебрав натуральные значения y от1 до 9, убеждаемся, что этой системе удовлетворяют лишь пары (1; 3), (7; 6). Итак, условиям задачи удовлетворяют три числа 630, 135, 765.
Практическая часть
Задача 1. Сумма первых пяти членов арифметической прогрессии на 200 больше суммы следующих пяти ее членов. На сколько сумма первых десяти членов этой прогрессии больше суммы следующих десяти ее членов? (Ответ: на 800)
Задача 2. Решите уравнение: (x + 1) + (x + 5) + (x + 9) +…+ (x +157) = 3200. (Ответ: x = 1)
Задача 3. Найдите сумму всех натуральных чисел, не превосходящих 200, которые при делении на 5 дают в остатке 3. (Ответ: 4020)
Задача 4. Три числа образуют
геометрическую прогрессию. Если среднее из них
удвоить, то получится арифметическая прогрессия.
Чему равен знаменатель q этой прогрессии,
если известно, что ![]() ? (Ответ:
? (Ответ: ![]() )
)
Тема 7. Задачи практического применения с геометрическим содержанием
Пример. Балкон имеет форму прямоугольника. С двух меньших сторон он утеплен одним слоем утеплителя, а с третьей стороны- двумя слоями. Площадь всего балкона 8 м2.После утепления балкон имеет размеры 3,6 м и 1,8 м. Какую толщину имеет слой утеплителя? Выберите уравнение, соответствующее условию задачи.
Задача 1. Найдите периметр прямоугольного участка площадью 252 м2, одна из сторон которого больше другой на 4 м. Ответ: 64 м.
Задача 2.На одном и том же расстоянии от стен комнаты прямоугольной формы площадью 24 м2, находится ковер размерами 3м и 2 м .Каково расстояние от ковра до стен комнаты? Выберите уравнение, соответствующее условию задачи.
Задача 3. Необходимо покрасить стены складского помещения, имеющего форму прямоугольного параллелепипеда, в котором есть дверь, шириной 4 м и высотой 2,5 м. Определите количество краски (в литрах) , которую следует купить для покраски стен помещения полностью, от пола до потолка, если , на 1м2 окрашиваемой поверхности расходуется 0,2литра краски и краску покупают с запасом в 6% от окрашиваемой площади. Ответ: 625 литров.
Тема 8. Как можно обойтись без уравнений
Теоретическая часть
Существует целый ряд задач, в том числе встречающихся на экзамене, которые гораздо удобнее решать “арифметически”, чем “алгебраически”, т.е. можно обойтись без уравнений.
Приведем примеры таких задач.
Задача 1. От пристани А одновременно вниз по течению отправились катер и плот. Катер спустился вниз по течению на 96км, а затем повернул обратно и вернулся в пункт А через14ч. Найти скорость катера в стоячей воде и скорость течения реки, если катер встретил плот на обратном пути на расстоянии 24км от пристани А.
В основе решения этой задачи лежит следующее соображение. Если катер удаляется от плота или приближается к нему, то его скорость относительно плота равна скорости катера в стоячей воде, меняется лишь направление этой скорости. Значит, катер удаляется от плота за то же время, что и приближается к нему, т.е. путь в 96 км от А до В пройден за то же время, что и 72 км от В до встречи с плотом. Значит, скорости катера по течению и против течения относятся как расстояния, проденные катером по течению и против течения, т. е. 96 : 72 = 4 : 3. Время на путь от А до В и обратно равно 14ч.
Это время надо разделить пропорционально числам 3 и 4, чтобы узнать время туда и обратно. Значит от А до В катер шел 6ч, а обратно – 8ч. Скорость по течению 96:6=16км/ч; против – 96:8=12км/ч. Скорость течения реки 0,5(16-12)=2км/ч, Скорость катера в стоячей воде 14км/ч.
Задача 2. Имеется два слитка золота массой 300г и 400г с различным процентным содержанием золота. Каждый слиток нужно разделить на две части таким образом, чтобы из получившихся четырех кусков можно было изготовить два слитка массой 200г и 500г с равным процентным содержанием золота. На какие части следует разделить каждый слиток?
Решение.В новых слитках (200г и 500г) процентное содержание должно быть таким же, как и в 700-граммовом слитке, получившемся при сплавлении исходных слитков. Отношение, в котором в каждый новый входят части исходных 3:4.