Множества в школьной математике ведут себя примерно так же, как обитатели леса: мы их почти не видим, но знаем, что они есть.
В классах с углубленным изучением математики основные понятия теории множеств рассматриваются достаточно подробно. Например, в [1] им посвящена глава "Элементы теории множеств". Ученик, изучивший эту главу, сможет лучше ориентироваться в других разделах математики.
Для обычного класса такую подготовку провести трудно, даже если содержание упомянутой главы значительно сократить. Слишком много новых терминов, чисто абстрактных рассуждений и специфической символики. Да и количество часов по программе не позволяет вводить дополнительную тему. Но если ученика математического класса можно сравнить с опытным охотником, который уверенно идет по лесу, то ученику обычного класса нужен хотя бы определенный минимум знаний по теории множеств, чтобы не заблудиться в трех соснах.
В обычных классах множества только изредка упоминаются. Чтобы сильные ученики смогли, тем не менее, овладеть нужными знаниями, возможно, например, изучать элементы теории множеств на факультативных занятиях. Но все-таки по возможности основные сведения должны получить все дети.
Решительный шаг в этом направлении сделан в последнем издании учебника по алгебре для 8 класса [5]. В прежних изданиях в разделе "Квадратные корни" назывались основные числовые множества (натуральные числа, целые, рациональные, действительные). Вводился знак принадлежности. Сейчас к этому добавилось определение подмножества (и знак включения). Говорится о взаимно однозначном соответствии между точками на прямой и действительными числами.
В теме "Неравенства" помимо рассмотрения числовых промежутков введен параграф "Пересечение и объединение множеств". Если раньше данным терминам уделялось немного внимания при рассмотрении промежутков, то теперь ученик сможет более детально ознакомиться с операциями над множествами. С недавних пор появился новый предмет "Теория вероятностей и статистика". Как раз в курсе теории вероятностей для 8 класса [6] при изучении алгебры событий говорится о правиле суммы и произведения, демонстрируются в качестве иллюстраций круги Эйлера. Нам представляется, что если ученик к этому времени будет знать, что такое вообще объединение и пересечение множеств (а не только для числовых множеств), то и в теории вероятностей объединение, пересечение событий этот ученик встретит как своих знакомых.
Но хотелось бы отметить, что само понятие множества в [5]подробно не обсуждается. По-видимому, авторы учебника допускают, что интуитивно ученик понимает это слово, первый раз встречаясь со словами "множество натуральных чисел" и т.д. Практика показывает, что это не так. У детей в первую очередь срабатывает реакция на названия "натуральные", "целые" и т.д. Они стараются их не перепутать, особенно "рациональные", "иррациональные", "действительные". Хотя предварительные сведения об этих числах встречаются уже в 6 классе, все равно для некоторых детей они оказываются трудными: во-первых, сами названия непростые, во-вторых, использование этих названия не так уж часто.
А смысл слова "множество" отходит при этом на второй план, некоторые дети автоматически связывают его со словом "много". Показателен вопрос, который растерянно задала мне одна восьмиклассница: "Как же множество может быть пустым? Ведь это же - множество!" Иногда путают слова "множество" и "количество". Скажем, когда детям нужно было привести пример множества, я в одной тетради прочитала: "Расстояние от Москвы до Петербурга". Поэтому для того, чтобы слово "множество" как математический термин хоть немного стало понятным, нужно как можно больше примеров и их обсуждения. Ученик должен привыкнуть к новому термину. Это произойдет только тогда, когда он начнет самостоятельно использовать его в своей речевой деятельности, пускай и в самых простых ситуациях. И только потом можно переходить к следующим темам, например, изучать пересечение и объединение множеств.
Чтобы понятие множества более органично воспринималось детьми, я посвящала ему отдельный урок в теме "Неравенства". На следующем уроке вводилось определение подмножества, рассматривалось число подмножеств конечного множества. Затем изучались операции над множествами, Эти уроки предшествовали занятиям по теории вероятностей.
Учитывая состав класса, я старалась максимально доходчиво вводить новые термины, но при этом стремилась не перегружать учащихся формальными выкладками, а добиваться понимания общих сведений. У меня было два восьмых класса. В одном, гимназическом, занимаются дети с более широким кругозором, они более восприимчивы к тому, что касается истории математики, к проблемам современной науки. На уроке в этом классе я приводила больше примеров с бесконечными множествами. Стараясь не перегружать учеников дополнительной терминологией, я показывала им интересные примеры со взаимно однозначным соответствием между множествами, которые иллюстрируют поразительный факт - часть может быть такой же, как целое. Слово "мощность" при этом намеренно старалась не называть. Мне кажется, что хотя бы на интуитивном уровне главная идея этих примеров детям все равно будет понятна.
В другом классе ученики не такие подготовленные. Им, скажем, сложно было воспринимать даже само слово "множество", потому что они с трудом могли настроиться на то, что это математический термин, а не обычное слово "множество", то есть "много". Поэтому для них я готовила больше простых конкретных примеров.
В презентации я использовала тот образ множества, который предложил Н.Н. Лузин: "Представим прозрачную непроницаемую оболочку, нечто вроде закрытого прозрачного мешка. Предположим, что внутри этой оболочки заключены все элементы данного множества и что, кроме них, внутри оболочки никаких других предметов не находится"[1].
Тем самым мы фиксируем элементы данного множества, а оболочка показывает, что они собраны в одно множество. Когда мы записываем множество с помощью фигурных скобок, именно эти скобки подчеркивают, что данные элементы составляют множество.
Поэтому на слайдах некоторые множества изображены как будто помещенными в прозрачные шары.
В данной статье представлен материал к уроку "Введение понятия множества".
Ключевые слова: "Множество, элемент множества, пустое множество, конечные и бесконечные множества".
В 70-х годах ХIX века немецкий математик Г. Кантор создал новую область математики - теорию бесконечных множеств. Через несколько десятилетий почти вся математика была перестроена на теоретико-множественной основе.
Понятия теории множеств отражают наиболее общие свойства математических объектов.
Мы только начинаем знакомиться с множествами.
(Слайд 3)
Множество - неопределяемое понятие в математике. С неопределяемыми понятиями мы уже встречались, например, в геометрии (прямая и точка). Множество можно представить себе как совокупность некоторых элементов.
Например, можно говорить о множестве цветов, которые растут на клумбе около нашей школы. Или о множестве точек на плоскости. Элементы множества могут быть любыми!
(Слайд 4)
Рассмотрим множество, которое состоит из
чисел 1, 2, 3, 4, 5. Обозначим это множество А.
Используется такая запись: А={1, 2, 3, 4, 5}. Число 1 -
элемент данного множества. Можно сказать и так:
"1 принадлежит множеству А". Есть специальный
значок принадлежности: 1![]() А Тот факт, что, скажем, число 7 не
принадлежит множеству А, записываем следующим
образом: 7
А Тот факт, что, скажем, число 7 не
принадлежит множеству А, записываем следующим
образом: 7![]() А.
А.
Говоря о множестве А, мы просто перечисляли его элементы. Иногда это отнимает много времени. Иногда вообще такое перечисление невозможно.
Рассмотрим множество всех положительных чисел. Пусть это множество В. С одной стороны, мы не в состоянии перечислить все элементы множества В, их бесконечно много, но, с другой стороны, мы понимаем, о каком множестве идет речь: с положительными числами мы хорошо знакомы - это числа, которые больше нуля. Записываем данное множество так: В={x|x>0}.
(Слайд 5 )
Дополнительные вопросы. Существует ли в этом множестве наибольший элемент? Приведите примеры элементов этого множества, которые меньше 1; 0,1; 0,01; 0,001. Существует ли наименьший элемент этого множества? Будет ли принадлежать этому множеству число 0?
На этом примере показано, что мы можем задать множество, описав самое важное свойство его элементов (оно называется характеристическим свойством множества). По этому свойству можно точно понять, из каких элементов состоит данное множество. Если нам удается это свойство сформулировать, то не нужно тратить время на перечисление элементов множества. Указав множество цветов, растущих на школьной клумбе, мы не обязаны перечислять все цветы. Мы только указали, где они находятся.
Таким образом, множества могут быть заданы по-разному. Самое главное, чтобы было понятно, какие именно элементы принадлежат данному множеству, а какие не принадлежат. Элементы могут быть любые, их порядок не важен.
(Слайд 6)
Если два множества состоят из одних и тех же элементов, мы их считаем равными. Пусть множество М состоит из элементов: квадрат, трапеция, пятиугольник, круг, треугольник. Множество Р: круг, квадрат, треугольник, пятиугольник, трапеция. Будут ли множества М и Р равны? Ответ поясните.
Отметим, что здесь мы обсуждаем множество именно как математическое понятие. Но ведь в нашем обычной речи тоже встречается слово "множество"! Важно их не перепутать. "Математическое" множество вовсе не обязано состоять из большого количества элементов. Множество может содержать и всего один элемент. Например, пусть множество D состоит из моей птицы Чир. И даже может быть так, что в множестве вообще нет никаких элементов!
(Слайд 7)
Множество, в котором нет ни одного элемента,
называется пустым множеством. Обозначение: ![]() . Например,
множество говорящих рыб - пустое. Пустым будет
множество корней уравнения 0х=3. Или, например,
множество параллелограммов, в которых все углы
острые.
. Например,
множество говорящих рыб - пустое. Пустым будет
множество корней уравнения 0х=3. Или, например,
множество параллелограммов, в которых все углы
острые.
О некоторых множествах трудно сразу сказать, пусты ли они или нет. Например, знаменитая проблема Ферма была решена только в 90-х годах ХХ века: было доказано, что не существует натуральных чисел n, больших двух, при которых уравнение xn+yn=zn имеет целочисленные положительные решения, то есть множество таких n пусто.
Приведите сами примеры различных пустых множеств.
Среди всех множеств выделяют конечные множества и бесконечные.
(Слайд 8)
В конечном множестве число его элементов всегда можно выразить определенным числом (иногда, правда, это число не так-то просто найти).
Приведем несколько примеров.
- Множество из 4 элементов: M={a;b;c;d}
- Множество цифр. Это множество из 10 элементов (назовите их!).
- Множество букв русского алфавита. Сколько в нем элементов?
- Множество всех тигров, живущих на Земле. К сожалению, тигров на Земле осталось очень мало. Экологи постоянно следят за их численностью.
(Слайд 9)
Рассмотрим множество, состоящее из гласных букв. Сколько в нем элементов?
Будет ли это множество равно множеству, состоящему из цифр?
А в некоторых случаях даже представить себе конечность множества нелегко. Вычислительная техника стремительно развивается. Компьютер отвечает на наши повседневные вопросы очень быстро, иногда нам кажется, что мгновенно. И действительно, объем информации, которую может обрабатывать современный компьютер, громадно. Однако и возможности компьютера ограничены, то есть конечны. В начале ХХI века стали заметны серьезные проблемы. Оказалось, что есть несколько принципиальных (непреодолимых) барьеров: атомная структура вещества, ограничение скорости света, туннельный эффект и проблема отвода тепла (перегрев процессора). Современный процессор по своим размерам постепенно приближается к атому! Но меньше атома процессор быть уже не сможет. А сейчас самая передовая технология дает отличие от размеров атома всего на три порядка! По прогнозам ученых, к 2017 году при аналогичных методах развития наступит предел - процессор уже нельзя сделать меньше.
Перед человечеством встали задачи, которые можно решить с помощью существующих компьютеров только теоретически. В реальности на их решение потребуется время, сравнимое со временем существования Вселенной [3].
Математики и другие ученые предлагают ответы на то, как обойти эти барьеры и ищут новые решения.
В истории математики было много случаев, когда вновь созданная теория воспринималась сначала слишком искусственной, а потом приобретала важнейшее практическое значение. Так было и с теорией бесконечных множеств. А сейчас теория множеств - это "каркас современной математики, она не всегда хорошо видна, но обеспечивает прочность всей конструкции" [4].
(Слайд 10)
Бесконечные множества. В них количество элементов выразить конечным числом невозможно.
Примеры бесконечных множеств:
- Множество всех положительных чисел.
- Множество всех точек на прямой.
- Множество всех треугольников.
- Множество всех фигур на плоскости.
(Слайд 11)
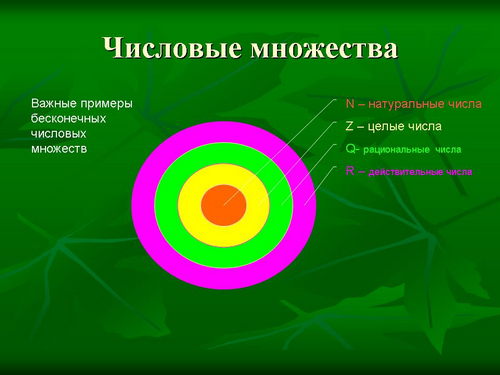
Нам уже известны самые важные числовые множества: N, Z, Q, R. Мы знаем, что натуральные числа - часть целых, целые числа составляют часть рациональных, рациональные - часть действительных. Как называются действительные числа, которые не рациональны?
Пусть даны числа 28; -15; 0,9; ![]() .
.
Запишите для каждого числа, принадлежит ли оно множествам N, Z, Q, R.
Попробуйте привести примеры множеств из геометрии, которые можно было бы проиллюстрировать аналогичной диаграммой (см. слайд: одно множество - часть другого).
(Слайд 12)
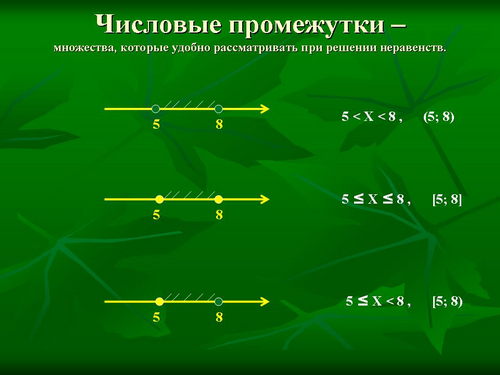
Мы уже знакомы с понятием "числовые промежутки". Это тоже множества.
Рассмотрим некоторые из них . Назовите несколько чисел, принадлежащих промежутку (5;8). Принадлежит ли этому промежутку число 8? Число 7,999? А можно ли назвать число из этого промежутка, которое больше 7,999? Есть ли на промежутке (5;8) самое большое число? Самое маленькое число?
Как вы думаете, сколько всего действительных чисел на промежутке (5;8)? Сколько на нем целых чисел? Назовите их.
Аналогичные вопросы можно рассмотреть для промежутков [5;8], [5;8).
В мире бесконечного мы встречаем много удивительного. Например, мы рассмотрели совсем небольшие, казалось бы, промежутки, а действительных чисел на них бесконечно много! Вспомним известный нам график - гиперболу. Что удивительного в гиперболе? А то, что она, приближаясь к осям координат, никогда не пересекает их. Но становится к ним все ближе и ближе! Как это возможно? Математики на это дали ответ (правда, далеко не сразу). Можно сравнить это настойчивое стремление с тем, как человек все время стремится к идеалу, но никогда его не достигает, а стремиться нужно!
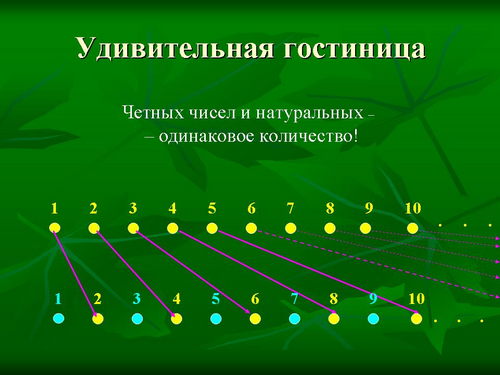
Другой удивительный пример из мира бесконечного. Мы привыкли к тому, что часть всегда меньше целого. А с бесконечными множествами иногда получаем другую картину. Рассмотрим натуральные числа и четные числа. Казалось бы, раз четные числа - это только часть натуральных, то четных должно быть меньше. А получается, что их столько же, сколько и натуральных!
(Слайд 13)
Допустим, что в фантастической гостинице (аналогичный пример приведен в [1]) бесконечно много номеров, все они заняты гостями из разных галактик - значит, этих гостей столько же, сколько номеров, то есть столько же, сколько натуральных чисел. И приезжает еще много гостей, нужно их разместить. А ведь все номера заняты, что же делать? Директор очень вежливо просит прежних постояльцев перейти в другие номера: если у прежнего гостя был номер 1, то этот гость переходит в номер 2, номер 2 - в номер 4, то есть все прежние номера меняются на номера, в два раза большие. Тогда освобождаются все нечетные номера! И их бесконечно много! Гостиница готова к приему новых туристов. А в четных номерах живут постояльцы, которых столько же, сколько натуральных чисел. С другой стороны, если новые туристы быстро уедут, то прежние могут вернуться в свои номера. И тогда получается, что четные числа благополучно "размещаются" по номерам 1,2,3:. Таким образом, мы установили взаимно однозначное соответствие между множеством натуральных чисел и множеством четных чисел. Четных чисел и натуральных - одинаковое количество.
(Слайд 14)
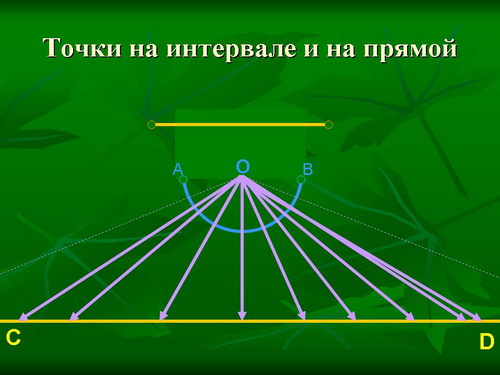
Похожим образом можно показать, что количество точек на промежутке (5; 8) такое же, что и на всей прямой. Изменим форму промежутка так, чтобы получилась дуга, полуокружность (но без граничных точек А и В) - эта дуга изображена на слайде. Пусть О - центр окружности, АВ - диаметр. Нашу прямую (обозначим ее СD) расположим так, чтобы она была параллельна АВ. Из точки О можно провести бесконечно много прямых, которые будут пересекать дугу, и при этом каждая из этих прямых пересечет нашу прямую СD. Можно представить себе, что каждая точка дуги "переезжает" в точку на прямой CD (по прямой, идущей из т. О и пересекающей СD - пути "переезда" изображены на слайде стрелками). И наоборот: для каждой точки прямой СD есть соответствующая на дуге. Таким образом, точек на дуге и на всей прямой - одинаковое количество, а, значит, оно будет одинаковым и для промежутка, и для прямой.
Дополнительные вопросы.
Почему нужно было расположить прямую CD параллельно АВ? Укажите прямую, которая пройдет через точку О, но не пересечет дугу. Не забудьте, что мы рассматриваем дугу без концов!
Более трудный вопрос. Можно ли аналогичным образом устроить "переезд" точек для [5; 8], [5; 8)? Замечаем, что "мешают" граничные точки. С теми ребятами, кого заинтересует эта задача, мы обсудим ее на факультативном занятии.
Для всех множеств (и конечных, и бесконечных), мы должны научиться определять, какие элементы принадлежат данному множеству, а какие нет.
(Слайд 15)
Рассмотрим два множества, А и В. Пусть множество А состоит из параллелограмма, трапеции, треугольника, квадрата. Множество В состоит из круга, квадрата, треугольника, пятиугольника, трапеции.
- Назовите общие элементы этих множеств.
- Какие элементы множества А не принадлежат множеству В?
- Какие элементы множества В не принадлежат множеству А?
- Назовите элементы, которые входят хотя бы в одно из данных множеств.
(Слайд 16)
Итак, мы познакомились с понятием множества, говорили об элементах множества. Узнали, что есть пустое множество. Множества бывают конечные и бесконечные. На следующих уроках мы узнаем о том, что с множествами можно производить некоторые действия (как и с числами - этим они немножко похожи друг на друга). Будем и дальше изучать множества! Они нам помогут лучше разобраться с другими задачами.
Литература.
- Виленкин Н.Я. Рассказы о множествах. - М.: Наука, 1965.
- Виленкин Н.Я.и др. Алгебра для 9 класса. - М.: Просвещение, 1996.
- Губайловский В. Наука будущего. Классические и квантовые компьютеры. //"Новый мир", 2011, №7.
- Жарковская Н.А. Георг Кантор и теория множеств. //"Курсор. Международный математический конкурс-игра "Кенгуру"". 2011, выпуск 5
- Макарычев Ю.Н. и др. Алгебра. 8 класс.- 19-е изд. - М.: Просвещение, 2011.
- Тюрин Ю.Н. и др. Теория вероятностей и статистика, - Москва, МЦНМО, 2008.