В предыдущих очерках, [3], [4] рассказывалось о реализуемой в ГОУ школа интернат “Интеллектуал” программе углублённого интенсивного обучения математике способных детей, начиная с первого класса. В этой статье мы продолжим рассказ о ходе этого эксперимента, описывая процесс обучения второклассников и третьеклассников за период с января 2012 по январь 2013. Параллельно этому, автор повторяет эту же программу с набором 2011 года из 16 нынешних второклассников. Как отмечалось в [4], осенью и весной 2011/2012 г. мы отбирали детей в наш очередной первый класс, который должен был начать обучаться у нас с 1 сентября 2012 г. К сожалению, через неделю после того, как наш директор поздравил счастливых родителей с поступлением их чад в нашу школу, он был вынужден, под давлением начальника Департамента образования Москвы, отменить приём в первый класс.
Мы в прошлый раз остановились на положении дел на 26 января 2012 г.
С тех пор, с конца января 2012 по настоящее время (16 января 2013) мы сделали следующее продвижение в нашем изучении математики.
Геометрия.
Доказаны следующие утверждения:
- а) отрезок, соединяющий середины боковых сторон
антитрапеции параллелен её основаниям и равен их
полуразности (геометрическое и векторное
доказательства)
б) отрезок, соединяющий середину одной из боковых сторон антитрапеции с точкой на другой боковой стороне и параллельный её основаниям, является её средней линией;
в) неверно, что отрезок, соединяющий боковые стороны антитрапеции, параллельный её основаниям и равный полуразности этих оснований обязательно является её средней линией. - Медианы треугольника пересекаются в одной точке.
- Биссектрисы треугольника пересекаются в одной точке (центре вписанной окружности).
- Серединные перпендикуляры треугольника пересекаются в одной точке (центре описанной окружности).
- Высоты треугольника пересекаются в одной точке (ортоцентре).
- Вписанный угол треугольника равен половине соответствующего центрального угла; угол с вершиной внутри круга равен полусумме дуг, высекаемых на окружности его лучами и лучами угла, ему вертикального; угол с вершиной вне круга равен полуразности дуг, высекаемых на окружности его лучами и лучами угла, ему вертикального. Угол, опирающийся на диаметр — прямой.
- Решены некоторые, вытекающие из вышеприведённых результатов, задачи на построение циркулем и линейкой.
Алгебра.
Были введены понятия высказывания, рассмотрены бинарные операции с высказываниями (конъюнкция, дизъюнкция, импликация) и унарная (отрицание).
Рассмотрены примеры высказываний и предложений, не являющихся высказываниями, построения отрицаний к данным высказываниям, конструированию сложных высказываний и определение истинности сложного высказывания.
Дети научились составлять таблицы истинности логических функций двух и трёх логических переменных. После составления таблиц основных логических тождеств, научились пользоваться ими для проверки того, не является ли данная логическая функция тавтологией. Научились составлять логические функции по заданным их значениям (нормальную дизъюнктивную форму).
Таблица основных логических тождеств

После ознакомления с исчислением высказываний, мы перешли к алгебре множеств. Ознакомились с понятиями подмножества, операциями дополнения, объединения и пересечения, научились доказывать теоретико-множественные тождества сведением их к логическим. Составили таблицу основных теоретико-множественных тождеств, двойственную к таблице логических тождеств.
Таблица основных теоретико-множественных тождеств

Проверяли правильность выводов построением диаграмм Венна. Вывели и научились применять к задачам практического содержания формулу включения-исключения для двух множеств.
На этом мы с ними остановились — наступило лето. Но, как и раньше, этот перерыв не стал для них временем полного отдыха от математики. Ученики получили комплект из 32 задач по материалу, пройденному за год с тем, чтобы за лето они не позабыли всё бесповоротно и окончательно, а, наоборот, повторили и закрепили полученные в течение учебного года навыки.
Вспомнив быстренько, с возобновлением занятий, материал предыдущего года, мы начали новый учебный год с продолжения темы “множества”.
Ввели понятие произведения множеств и доказали связанные с ним тождества. Ввели понятие “бинарное отношение”, заданное на квадрате множества и рассмотрели типы этих отношений: свойства отношения быть (или не быть) рефлексивным, симметричным и транзитивным. Нашли примеры для всех 8 возможных вариантов отношений относительно этих свойств.
| число | RST | Множество и отношение в нём |
0 |
000 | |
1 |
001 | |
2 |
010 | |
3 |
011 | |
4 |
100 | |
5 |
101 | |
6 |
110 | |
7 |
111 |
(Отношение типа 1 – отношение строгого порядка; отношение типа 3 – отношение нестрогого порядка, отношение типа 7 – отношение эквивалентности).
Далее, основным примером отношения эквивалентности стало разбиение целых чисел по модулю какого-то выбранного натурального числа. Ввели и проверили на корректность операции сложения и умножения в полученном фактор-множестве, и получили конечные арифметики (арифметики остатков по модулю натурального числа).
Вывели основные правила:
amodc[+]bmodc![]() (a+b)modc
и amodc[
(a+b)modc
и amodc[![]() ]bmodc
]bmodc![]() (a
(a![]() b)modc,
b)modc,
где в квадратные скобки заключены арифметические действия с классами чисел, а без — обычные арифметические действия с целыми числами. На основании второго из них получен способ быстрого определения остатка от степени числа и получен навык в решении упражнений типа: найти остаток от деления на 8 суммы чисел 5300+11500.
Далее, мы ввели понятия простых и составных чисел и с помощью процедуры “решета Эратосфена” выявили простые числа в пределах от 2 до 61.
Затем обсудили вопрос, до какого простого делителя нужно проверять неизвестное число, чтобы убедиться в том, что оно — простое.
После этого вывели признаки делимости в десятичной системе на 2, 4, 8, 5, 25, 10, 3,9,11.
Поупражнялись в разложении чисел на простые множители.
После этого научились, не производя деления узнавать остатки от деления на числа, являющиеся произведением этих делителей.
Типичными являются, например, следующие упражнения:
Найти 2094783mod15; 87365429mod44; 637652965mod99; 82701012873mod165.
Научились находить числа по заданным их остаткам от деления на заданные числа.
Рассмотрим модельную задачу:
в столовую привезли гору мандаринов из Абхазии.
Если раздавать каждому ученику по 5 мандаринов, то останутся два мандарина, если раздавать по 6 мандаринов, то останутся 4 мандарина, если раздавать по 7 мандаринов, то останется один мандарин, если раздавать по 8 мандаринов, то останется 6 мандаринов. Сколько учеников учится в этой школе?
Как обычно, обозначим неизвестное число
учеников буквой х и составим систему уравнений: 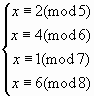
Начнём из одного уравнения подставлять х в
другое. Начнём с последнего (как наибольшего
делителя – 8): Х=8k+6, k=0,1,2, и подставим в
предпоследнее (поднимаемся снизу вверх): (8k+6)mod7![]() 1;
1;
8k(mod7)+6mod7![]() 1;
8mod7·kmod7+6mod7
1;
8mod7·kmod7+6mod7![]() 1;
kmod7+6mod7
1;
kmod7+6mod7![]() 1;
1;
добавим по 1; к обеим частям равенства: kmod7![]() 2;
2; ![]() k=2.
k=2.
Итак, мы нашли первый Х удовлетворяющий обоим уравнениям – последнему и предпоследнему: Х=8·2+6=22.
Последующие числа, удовлетворяющие этим двум
уравнениям, будут идти с периодом 7·8=56: Х=22+56m.
Подставим теперь это выражение для Х во второе
уравнение: (22+56m) mod6![]() 4; 22 mod6+(56 mod6)·(m mod6)
4; 22 mod6+(56 mod6)·(m mod6)![]() 4; 4mod6+2m(mod6)
4; 4mod6+2m(mod6)![]() 4; 2m
4; 2m![]() 0 (mod6)
0 (mod6) ![]() m=0. Итак, первым числом, удовлетворяющим
последним трём уравнением будет по-прежнему 22.
Только последующие будут идти теперь уже с
периодом 7·8·6=336; Х=22+336n. Подставляем найденное
выражение для Х в первое уравнение: (22+336n) mod5
m=0. Итак, первым числом, удовлетворяющим
последним трём уравнением будет по-прежнему 22.
Только последующие будут идти теперь уже с
периодом 7·8·6=336; Х=22+336n. Подставляем найденное
выражение для Х в первое уравнение: (22+336n) mod5![]() 2; 2 mod5+1·n mod5
2; 2 mod5+1·n mod5![]() 2; (n+2) mod5
2; (n+2) mod5![]() 2; n=0.
2; n=0.
Итак, число 22 удовлетворяет всем четырём условиям задачи. Но вряд ли правдоподобно выглядит такое маленькая школа, разве что малокомплектная в сельской местности. Следующим числом, удовлетворяющим этим условиям, будет 22+336·5=1702 ученика. Нормальная московская школа после слияния и объединения…
Научились находить НОД и НОК двух чисел разложением их на простые множители, и находя, соответственно, пересечение и объединение множества их простых делителей (с учётом кратности каждого делителя в разложении на множители).
Следующей целью нашей программы было ознакомление с так называемыми целочисленными задачами, неизвестными в которых являются целые числа. Поскольку никаких других чисел мы в третьем классе пока ещё не знаем. Построением дробей мы займёмся уже в конце февраля, после первых весенних каникул.
Привожу примерный список решаемых нами задач (мы находимся в процессе их решения на момент окончания этой статьи):
- Докажите, что х2+у2
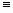 0mod3
0mod3 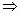 (x
(x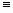 0mod3)
0mod3) 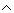 (y
(y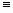 0mod3)
0mod3) - Докажите, что х2+у2
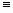 0mod7
0mod7 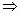 (x
(x 0mod7)
0mod7)  (y
(y 0mod7)
0mod7) - Докажите, что если к трёхзначному числу
приписать справа то же самое число, то полученное
шестизначное число
 будет кратно 7, 11 и 13.
будет кратно 7, 11 и 13. - К двузначному числу
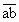 приписали слева и справа двойку.
Получилось число
приписали слева и справа двойку.
Получилось число 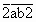 , которое в 32 раза больше исходного
числа.
, которое в 32 раза больше исходного
числа.
Каково же было исходное число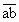 ?
? - Четырехзначное число оканчивается цифрой 4. Если эту четвёрку переставить в начало числа, то оно уменьшится на 1107. Найдите это число.
- Найдите двузначное число, которое при делении его на цифру его единиц даёт в частном цифру его единиц, а в остатке цифру его десятков.
- Докажите, что если любое двузначное число
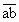 написать три
раза подряд:
написать три
раза подряд:  ,
то получившееся шестизначное число будет
делиться на 7.
,
то получившееся шестизначное число будет
делиться на 7. - Четырехзначное число
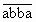 является кубом натурального числа.
Найдите это натуральное число (рассуждениями, а
не подбором!).
является кубом натурального числа.
Найдите это натуральное число (рассуждениями, а
не подбором!). - Докажите, что число
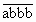 -a делится на 37.
-a делится на 37. - Найдите правильную положительную дробь, которая не изменится, если к числителю её прибавить некоторое натуральное число, а знаменатель умножить на это же число. Каково это число?
- Найди все целые значения m, при которых корень уравнения mx+5x=20 является натуральным числом.
- Найдите натуральные числа, разность квадратов которых равна 455.
- Если к задуманному числу приписать справа нуль и результат вычесть из числа 143, то получится утроенное задуманное число. Какое число было задумано?
И последней темой в этом, четвёртом учебном модуле будет у нас решение ребусов.
Прилагаю их примерный список для получения представления о трудности задач.
Предполагается, что решения записываются в виде строгой логической последовательности действий с использованием символов математической логики.
Разгадайте числовые ребусы. Одинаковым буквам соответствуют одинаковые цифры, разным буквам соответствуют разные цифры.
- АИСТ+АИСТ+АИСТ+АИСТ=СТАЯ
- УДАР+ УДАР=ДРАКА
- SEND+MORE=MONEY
- ЛЕТО+ЛЕТО=ПОЛЕТ
- НАТАША+ТОНЯ=СЕСТРЫ
- ВАГОН+ВАГОН=СОСТАВ
- ВЕТКА+ВЕТКА=ДЕРЕВО
- РАЙОН+РАЙОН=ГОРОД
- FORTY+TEN+TEN=SIXTY
- СИНУС+СИНУС+КОСИНУС=ТАНГЕНС)
- ОДИН+ОДИН=МНОГО
- ТАМТАМ+МРАК=КОШМАР
- ДЕТАЛЬ+ДЕТАЛЬ=ИЗДЕЛИЕ
- Д+АД+ЛАД+КЛАД+ОКЛАД+ДОКЛАД=987654
- АТАКА+УДАР+УДАР=НОКАУТ
- ПЛОМБА? 5=АПЛОМБ
- ЕINS? 5=FUNF
Главным позитивным результатом, достигнутым за прошедшие полтора гола, является сложившееся у школьников отношение к предмету: математикой занимаются с удовольствием, на уроках дети активны, стараются все, в том числе и те, у кого не очень получается. Математика является у них любимым предметом. Это лишний раз показывает, что не нужно оберегать детей от умственных нагрузок, от трудных, подчас кажущихся неразрешимыми задач. Мы склонны недооценивать возможности детей младшего возраста, и связано это, прежде всего, с неразвитостью их речевых навыков.
Учебник для первого класса уже реализуется ЦДО “Маяк” (www.mayakschool.ru), в котором занятия по этой программе и методике проводит моя ученица, Светлана Геннадиевна Берёзкина. Посмотреть видеоролик, показывающий моих учеников (тогда, соответственно, первоклассников и второклассников), снятый в апреле 2012, можно в YouТube по ссылке http://www.youtube.com/watch?v=PFzjZki1KF4
Литература
[1] Абрамсон Я.И.Преподавание математики (авторская программа) в НОУ "Школа Алеф" (2007 / 2008 учебный год), https://urok.1sept.ru/articles/511767/
[2] Абрамсон Я.И. Авторская программа преподавания математики в школе-интернате для одаренных детей "Интеллектуал" https://urok.1sept.ru/articles/579242/
[3] Абрамсон Я.И., Обучение одаренных детей математике. 1-й класс (2010 / 2011 уч/ год) https://urok.1sept.ru/articles/602405/
[4] Абрамсон Я.И., Обучение одаренных детей математике. 2-й класс (2011 / 2012 уч/ год) https://urok.1sept.ru/articles/619698/
[5] Абрамсон Я.И. Математика. 1 класс. Книга для учителя. Спб, 2012.