Тип урока: урок ознакомления с новым материалом и первичное его закрепление.
Цель урока: рассмотреть решение некоторых типов иррациональных уравнений; закрепить знания, умения и навыки решения иррациональных уравнений.
Задачи:
- формировать у учащихся умение решать иррациональные уравнения различными способами, отработать навыки решения иррациональных уравнений;
- развитие алгоритмического мышления, памяти, внимательности; операционного мышления, направленного на выбор оптимальных методов решений;
- развитие у учащихся умения излагать мысли, делать выводы, обобщения; развитие познавательного интереса, логического мышления, воспитывать умение преодолевать трудности при решении задач;
- усиление познавательной мотивации осознанием ученика своей значимости в образовательном процессе;
- воспитание у учащихся самостоятельности, способствовать выработке умения обобщать изучаемые факты.
Материал разработан применительно к учебнику “Алгебра и начала анализа, 10-11” под редакцией А.Н. Колмогорова.
Методы работы:
- наглядный,
- практический,
- проблемно-поисковый,
- метод самостоятельной работы,
- словесный
Формы работы учащихся: фронтальная, индивидуальная, самостоятельная.
Необходимое техническое оборудование: доска Smart Board, мультимедийный проектор, компьютерный класс с доступом в сеть Интернет, презентация (Приложение1).
План урока.
I. Актуализация (10 мин.)
- Проверка домашнего задания.
- Повторение пройденного материала.
II. Объяснение нового материала (10 мин.)
- Сообщение темы урока.
- Постановка целей и задач.
- Рассмотреть некоторые способы решения иррациональных уравнений.
III. Закрепление изученного материала (10 мин.)
IV. Подведение итогов (2 мин.)
V. Домашнее задание (2 мин.)
VI. Самостоятельная работа (10 мин.)
Ход урока
Здравствуйте, ребята. Улыбнитесь и подарите теплоту своих сердец друг другу.
Эпиграфом к нашему уроку я бы взяла слова великого учёного, математика Древней Греции Евклида: “Познание мира ведет к совершенствованию души”.
Действительно, для достижения духовного совершенства мы познаем мир. Мы изучаем теорию, методы решения задач и уравнений.
А начнём мы наш урок с проверки домашнего задания. Есть ли вопросы по выполнению?
Кто желает проверить свои знания по карточкам? / 2 ученика работают на доске, два получают разноуровневые карточки в форме лепестков ромашки, задания которых выполняют на месте на листочках /
Жёлтый лепесток ромашки - ![]() =3
=3
Зелёный - ![]() = х
= х
Синий ![]() =3
=3
Красный - ![]()
В учебной среде Телешкола сегодня работают ___________ откройте урок 8 на странице 2, выполните математический тренажер на оценку.
А с вами мы пройдёмся по дидактическим островкам.
Умение рассуждать логически важно в жизни каждого человека.
“Все наше достоинство в мысли!”. Паскаль
Воспользуемся нашим достоинством в теоретическом марафоне.
(Все остальные выполняют задания, спроектированные на доску.)
Учитель: Давайте напомним, какую тему мы начали изучать на прошлом уроке? Иррациональные уравнения.
- Какие уравнения называются иррациональными?
/ Иррациональными называются уравнения, содержащие переменную под знаком радикала./ - Какую практическую направленность имеет эта тема? / Необходимость изучения решения иррациональных уравнений очевидна, иррациональным уравнением выражаются формулы, описывающие многие физические процессы:
- равноускоренное движение;
- 1 и 2 космические скорости;
- среднее значение скорости теплового движения молекул;
- период радиоактивного полураспада и другие.
А так же иррациональные уравнения использует статистика..
Учитель: Вы правы, а ещё не следует забывать, что в этом году вам предстоят сложные испытания – сдача государственного экзамена, а в работе эта тема всегда присутствует. Так что к ней нужно отнестись очень серьёзно.
Прошу вашего внимания на доску. Здесь расположены карточки, на которых записаны уравнения. Кто выберет среди данных уравнений иррациональные? Работа с интерактивной доской
/ Ученик работает с доской Smart Board – находит и перетаскивает карточки с иррациональными уравнениями /.
-Что значит решить уравнение? / Решить уравнение – значит найти все его корни или доказать, что оно не имеют корней /
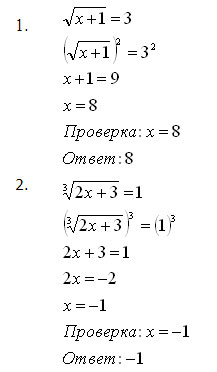
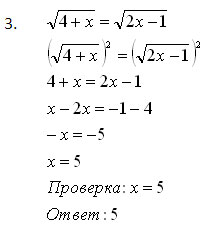
Каким способом мы решали эти уравнения? / Возведением обеих частей уравнения в степень, равную показателю степени/
Учитель: Кто сформулирует способ решения иррациональных уравнений? / Решение иррациональных уравнений сводится к переходу от иррациональных к рациональному путём возведения обеих частей в степень, равную показателю степени. Однако при этом возможно появление посторонних корней, значит, надо не забыть, при этом, сделать проверку./
Все ли иррациональные уравнения можно решить только этим способом? Перед вами следующее уравнение. Как будем решать это уравнение?
![]()
При возведение в куб обеих частей уравнения оно примет ещё более сложный вид.
Значит, наверное, есть более рациональный способ решения?
Как вы считаете, какие задачи стоят перед нами на сегодняшнем уроке?
/ Изучить новые способы решения иррациональных уравнений /.
Запишите в тетради число и тему урока: “ Иррациональные уравнения. Решение уравнений ”
И записываем задание № 4.
"Метод замены переменных" разбирается на примере решения уравнения. Начинает учитель, заканчивает ученик.
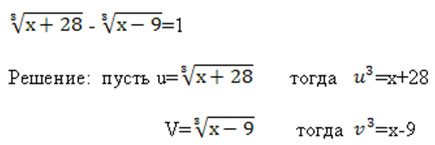
Получаем систему уравнений: 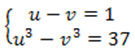 решив систему, получаем
решив систему, получаем ![]()
Итак, имеем два уравнения:
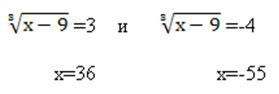
Ответ: 36; -55.
Таким образом, мы рассмотрели решение иррациональных уравнений методом замены переменных. Каков же план решения уравнений этим способом? (Ученики участвуют в формулировке.)
Чтобы решить иррациональное уравнение методом замены переменных нужно:
- Вводим две неизвестные величины (и,v)
- Составляем 1 уравнение в систему
- Возводим уравнения в степень (избавляемся от корня)
- Составляем 2 уравнение в систему (избавляемся от x)
- Решаем систему, находим и или v
- Решаем простейшее уравнение, записываем ответ.
Закрепление
Далее ученикам предлагается решить следующие уравнения:
№1 ![]()
Решение: пусть 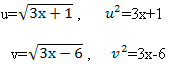
Получаем систему уравнений:
![]()
итак, u=4
![]()
3х+1=16
х=5
Проверка: х=5 корень
Ответ х=5
Физкультминутка
Сегодня я бы хотела показать вам еще один способ решения иррациональных уравнений. Это функционально- графический способ. Так как этот способ дает нам не точные значения переменной, то его используют реже. Однако встречаются уравнения, которые можно и легче решить именно этим способом. Посмотрите, как это делается. Внимание на экран.
Показываю презентацию
Решить уравнение ![]() (рис. 1, 2, 3).
(рис. 1, 2, 3).
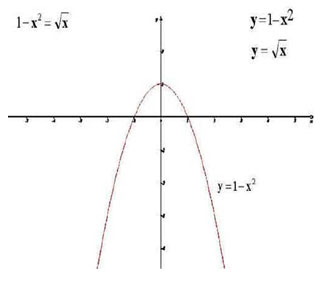
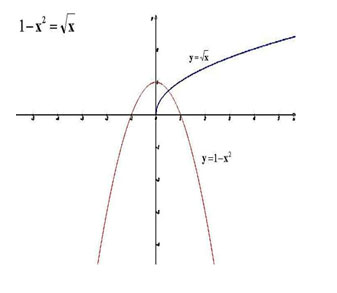
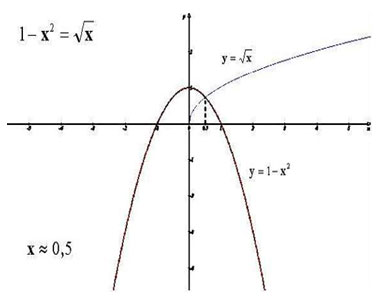
IV. Работа по группам.
А теперь проведём тестирование.
5 человек работают на компьютере на рабочем столе папка “Тестирование” остальные на месте выполняют самостоятельную работу по карточкам.
Самостоятельная работа

Ответы:
| № варианта | 1 | 2 | 3 |
| Вариант 1 | 8 | 0; 4 | 0; 3; 4 |
| Вариант 2 | 5 | 0; -1 | 0; -2 |
Итоги урока: Итак, ребята!
– Какие способы решения иррациональных уравнений мы рассмотрели?
Давайте обсудим достоинства и недостатки рассмотренных способов.
1. Метод возведения обеих частей уравнения в одну и ту же степень, что и степень корня
Вывод: При решении иррациональных уравнений
методом возведения обеих частей уравнения в одну
и туже степень необходимо вести словесную
запись, что делает решение понятным и доступным.
Однако обязательная проверка иногда бывает
громоздкой и занимает много времени. Этот метод
можно использовать для несложных иррациональных
уравнений, содержащих 1-2 радикала.![]()
2. Функционально графический метод
| Достоинства | Недостатки | |||
| 1. Наглядность | 1. Словесная запись | |||
| 2. Если ответ точный, то нужна проверка. | 2. Ответ может быть приближенным, не точным |
Вывод: Функционально графический метод – это наглядный метод, но применять его лучше тогда, когда легко можно построить графики рассматриваемых функций и получить точный ответ. Если ответ приближенный, то лучше воспользоваться другим методом.
3. Метод введения новых переменных
Вывод: Этот метод лучше применять для иррациональных уравнений, содержащих радикалы различных степеней, или одинаковые многочлены под знаком корня и за знаком корня, или взаимообратные выражения под знаками корня.
Учитель: Вы видите, что для каждого иррационального уравнения необходимо выбирать наиболее рациональный способ решения: понятный, доступный, логически грамотно оформленный.
Продолжите фразы:
Мне было интересно…. Мне было трудно… Мне было непонятно… Свою работу я оцениваю как … Я научился… Я надеюсь… Я думаю…. Я считаю…
Я желаю Вам достичь заветной цели, а главное стремиться к постоянному самосовершенствованию.
“Да, мир познания не гладок.
И знаем мы со школьных лет
Загадок больше, чем разгадок,
И поискам предела нет!”
Сегодня на уроке вы поработали, поэтому за работу на уроке сегодня получают оценки
Домашние задания сегодня вы получаете в пяти вариантах. Задания данной работы соответствуют прототипам заданий 6 из открытого банка заданий ЕГЭ по математике. Считаю, что это будет полезно каждому для подготовки к экзаменам. Приложение 2