Цель: Показать применение методов теории вероятности и статистики на уроках физики при выполнении лабораторных работ.
Задачи урока
Образовательные:
- Повторить понятия среднего арифметического и дисперсии измеряемой величины;
- Вспомнить абсолютную и относительную погрешности измерений,
- Применить полученные знания при выполнении физических задач;
- Установить метапредметные связи.
Развивающие:
- Развитие логического мышления, умения делать выводы;
- Развитие умения применять информационные технологии для оформления работ и решения задач с современными требованиями.
Воспитательные:
- Стимулирование познавательной деятельности постановкой соответствующих вопросов и заданий;
- Воспитание навыков групповой работы.
Планируемые результаты
Учащиеся должны знать и понимать:
- Основные определения теории вероятности и статистики;
- Физический смысл, которые приобретают известные из статистики величины в области естествознания.
Учащиеся должны уметь:
- Применять методы математической статистики к решению физических задач лабораторного практикума;
- Правильно оценивать полученный результат.
Тип урока: Интегрированный урок по математике - физике. Продолжительность - 2 час.
Технология: Работа в группах.
Комплексно-методическое обеспечение: Проектор, компьютер, лабораторное оборудование для практических заданий, калькуляторы.
План проведения урока:
1. Организационный момент. Постановка задач и цели урока.
2. Основная часть.
а) Повторение прямых и косвенных измерений, абсолютной и относительной погрешностей.
б) Применение теоретических знаний. Решение примера.
в) Практическая часть урока. Выполнение группами практических заданий по физике.
3. Подведение итогов. Рефлексия. Заключительное слово учителя.
Учитель физики. Здравствуйте! При измерении, например, размеров тела можно получить совершенно разные результаты. Почему? Измерения можно проводить разными приборами (линейками или рулетками), имеющими разную степень точности измерений. Наше время называют эпохой нанотехнологий. И это неслучайно. Механические способы измерений сменились оптическими, в результате чего точность измерений повысилась в 1000 раз. Тем не менее, теория измерений и обработки экспериментальных данных осталась прежней. Цель нашего урока – познакомиться с ее основами, научиться измерять и рассчитывать измеряемые величины правильно.
Учитель математики. Давайте вспомним основные моменты данной науки. Итак, измерение - это нахождение величины опытным путем с помощью средств измерений. Различают прямые и косвенные измерения. Прямое измерение – это определение значения величины непосредственно средствами измерения.
Учитель просит учащихся привести примеры прямых измерений. Ученики должны вспомнить, например, что измерение времени движения тела проводят обычно с помощью часов, массы тела - с помощью весов, объема жидкости - с помощью мензурки.
Учитель физики. Косвенное измерение – это определение величины с помощью формулы, связывающей ее с другими величинами, которые можно узнать прямыми измерениями. Вспомните, какие величины мы можем узнать, пользуясь формулами. Запишите их.


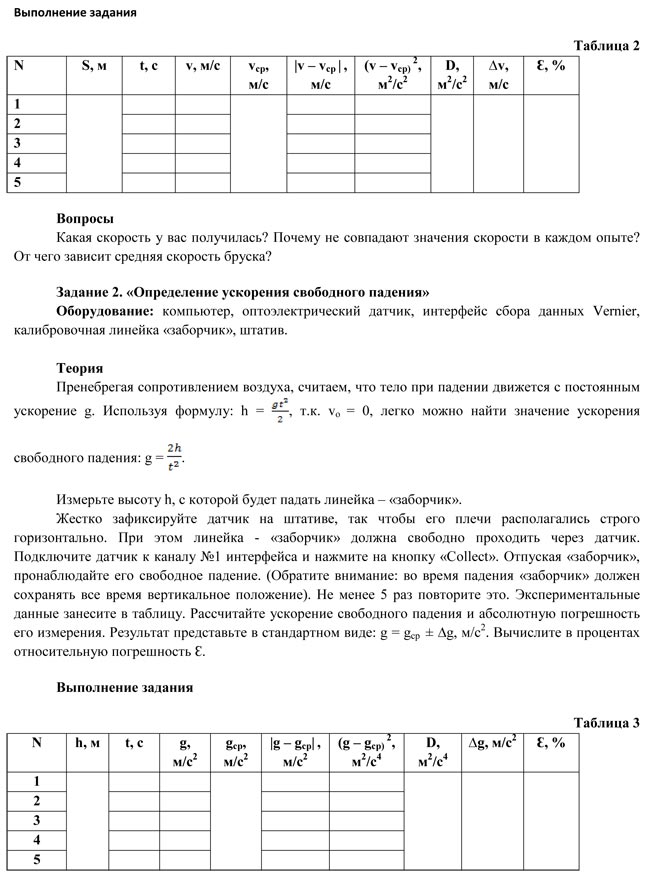
Вопросы
Как сильно отличается полученное значение g от общепринятого 9,81 м/с2? Входит ли общепринятое значение g в доверительный интервал? Изменится ли значение ускорения свободного падения, если высоту h уменьшить? увеличить? Как влияет на результаты определения g сила сопротивления воздуха?
Заключение
Учитель математики. Сегодня на уроке мы вспомнили основные моменты теории вероятностей и статистики, и, самое главное, попытались эти знания использовать на практике. Еще раз мы убедились, что между науками много общего. Математика дает нам инструмент, с помощью которого можно изучать, измерять, рассчитывать.
Учитель физики. Но, как сказал в свое время выдающийся физик XX века Альберт Эйнштейн, «единственным источником знаний является опыт», и хотя опыт берет за ученье большую плату (делать самим гораздо труднее), учит при этом лучше всех других учителей.
Литература
- Ю.Н. Тюрин, А.А. Макаров, И.Р. Высоцкий, И.В. Ященко. Теория вероятностей и статистика, МЦНМО, 2008.
- Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский; под редакцией Н.А.Парфентьевой. Физика. 10 класс: учебник для общеобразовательных учреждений. - М.: Просвещение, 2017.
- Н.А.Парфентьева. Физика. Тетрадь для лабораторных работ. 11 класс. Пособие для учащихся общеобразовательных организаций: базовый уровень. – М.: Просвещение, 2012.
- Физика с Vernier. ПКГ «Развитие образовательных систем», М., 2012.
- Зайдель А.Н. Погрешности измерений физических величин. – Л.: Наука, 1985.
- Тэйлор Дж. Введение в теорию ошибок. - М.: Мир, 1985.