Я преподаю дисциплину ОП.05 «Метрология, стандартизация, сертификация» студентам 3 курса, обучающимся специальности 23.02.03 «Техническое обслуживание и ремонт автомобильного транспорта» (23.02.07 «Техническое обслуживание и ремонт двигателей, систем и агрегатов автомобилей» – общепрофессиональный, сугубо технический предмет, необходимый для полноценного овладения МДК «Техническое обслуживание и ремонт автомобильного транспорта», в тесном контакте с преподавателями по ремонту а/м. При изучении дисциплины предусмотрен ряд лабораторных и практических работ.
Работа рассчитана на 2 учебных занятия (4 академических часа), но при недостатке учебного времени ее можно провести и за 2 часа. Однако, в этом случае анализ полученных результатов проводится в большой степени преподавателем, у доски, при активном диалоге с обучающимися.
Определение и анализ погрешностей измерения
Это последняя лабораторная работа в теме «Метрология», она завершает и обобщает теоретически и практически изученный материал. Рассчитана на 4 академических часа (2 пары):
- Практическая часть (измерения) и качественный анализ результатов
- Количественный анализ результатов, обсуждение и выводы.
Оценки выставляются на основании 3 факторов:
- Оценка за технику измерений, выставленная «экспертами»
- Оценка, предложенная бригадиром, отражающая вклад студента в общую работу
- Оценка, выставленная преподавателем за работу при анализе результатов.
Несмотря на то, что студенты, казалось бы, легко усваивают теорию измерений, в частности, понятие «погрешности измерений», на практике для них характерно идеалистическое восприятие: измерено – значит, точно. Если средство измерение градуировано до сотых – значит, оно достоверно измеряет с точностью до сотых, и, безусловно, точнее того, шкала которого градуирована до десятых. Изучив ранее основы теории измерений, студенты не воспринимают ее, применительно к практике. Тем не менее, при изучении тем, связанных с точностью, ее достижимостью, надо понимать разницу между достоверной и более или менее вероятной величиной.
Цели работы:
| Преподавателя (обучающие) | Студента |
|
|
А также |
|
|
|
Задачи работы
- Многократно измерить размер детали разными приборами, используемыми при ремонта а/м.
- Качественно оценить и количественно проанализировать полученные результаты;
- Выявить характер и причины погрешностей измерения и проанализировать их;
- Сформулировать доступные способы оценки достоверности измерений и повышения их точности.
Методы работы
- Анализ теоретической информации;
- Технические измерения (сбор и систематизация результатов);
- Анализ результатов и обобщение, принятие решений. При поиске способов уменьшения влияния случайных и систематических погрешностей – метод мозгового штурма.
Работа с аудиторией происходит в 3 формах:
- Фронтальная (постановка целей, задач, инструкции и т.п.) на начальном этапе и формулировка промежуточных задач и обобщение.
- Работа в малых группах, самостоятельная;
- Самостоятельная работа дома, в том числе с Интернетом.
Гипотеза
| С точки зрения неспециалиста | С точки зрения метрологии |
|
|
Практическая (лабораторная) часть
I занятие
Ход работы
Оргмомент (как обычно)
Группа разбивается на 3 бригады. В каждой выбирается бригадир и два «эксперта». Каждая бригада должна организовать измерение одного и того же размера минимум 20 раз разными людьми и обработать результаты измерения.
Задача бригадира – организовать и координировать работу, экспертов – записывать измеренные каждым студентом значения, оценивать его умение выполнять измерения – и все это без подсказок и комментариев. И следить, чтобы не сломали инструмент! На каждом ряду группируется бригада, им выдаю деталь и инструмент) (гильзу, распредвал и т.д., нутромер, микрометры). Место измерения (особенно, если деталь с большим износом, можно отметить мелом.
«Эксперты по нутромеру» собирают и настраивают его (т.к. это не быстро и непросто), пока организуем остальную часть работы. На доске рисуем 3 таблицы из 2 столбцов (№ измерения и размер) для каждой бригады, название детали и измерительный инструмент. Там, где нутромер – и размер настройки. Каждый в своей тетради пишет название работы и рисует таблицу «мои измерения». «Эксперты по микрометру» в это время поверяют, и, если надо, калибруют инструмент.
На первом столе в каждом ряду лежат деталь, измерительный инструмент и за столом сидят два эксперта ИЗ ДРУГИХ БРИГАД. Перед ними лежат заранее приготовленные таблицы для записи результатов. Они по очереди измеряют все 3 детали, записывают свои результаты в таблицы (естественно, вместо оценок – прочерк);
Далее все студенты, по очереди, измеряют эти детали. Каждый измеряет, называет результат эксперту, эксперт называет ему номер (по их таблице). Например, «номер измерения 16, размер 92,04». Студент записывает результат в свою таблицу, а потом – в соответствующую таблицу на доске. Соответственно, в оставшееся время надо переписать в свою тетрадь таблицу с результатами своей бригады. Разумно, если в каждой бригаде выделят одного человека, который обеспечит аккуратную запись результатов, одну на всех. Если студентов в группе мало, можно измерять и по второму разу.
Как только в последней из бригад набралось 20 измерений, работу прекращают все.
Бригады возвращаются, каждая - на свой ряд. Теперь надо обработать результаты.
Преподаватель берет «протоколы» (таблицы, заполненные экспертами). Теперь работа на доске. Считаем: Хmax – Xmin =? А какова допустимая погрешность измерения? Преподаватель предлагает оценить результаты, отбросив явно выделяющиеся из ряда, то есть явно с грубыми ошибками. В этом студентам надо помочь. При измерениях микрометром результаты могут группироваться вокруг двух центров, между которыми 0,5 мм. Отбросив явно ошибочные результаты, опять прикидываем погрешность измерения и сравниваем с нормативной.
Преподаватель в заключении занятия кратко анализирует характер распределения размеров, указывает на возможные причины погрешностей, спрашивает, как можно уменьшить влияние случайных погрешностей, и как – систематических?
Окончательный анализ и обсуждение результатов – на следующем занятии. Оценки выставляются на основании 3 факторов:
- Оценка за технику измерений, выставленная экспертами.
- Оценка, предложенная бригадиром, отражающая вклад студента в общую работу.
На дом:
- Привести в порядок записи, закончить график и т.д.
- Повторить тему «Погрешности измерения».
Занятие №2. Анализ погрешностей измерения
Аналитическая часть
1. Анализ результатов
Выполняется бригадой, совместно.
Если есть значения измерений, намного выбивающиеся из ряда и свидетельствующие о грубой ошибке, отметить их. Если они встречаются 1-2 раза, можно сразу отбросить их за недостоверностью. В протоколе измерений выделить наибольшее и наименьшее значение, рассчитать диапазон разброса размеров и разделить на 6-9-12 интервалов.
Преподаватель сам выбирает интервалы, число измерений в которых каждой бригаде надо подсчитать. Если Хmax – Xmin около 0,1 или меньше, то интервал проще взять 0,01, если много больше, то удобно, если их будет 9 или 12.
Например, 81,76 – 81,99 = 0,23 Почти 0,24, интервал 0,02 мм.
Студенты считают число измерений в каждом интервале. Работа коллективная, то есть, например, один считает первый, другой – второй. В результате строим график. Обычно получается или нечто, напоминающее нормальное распределение, или же «двугорбый верблюд». Другие варианты – редкость.
Хmax – Xmin =______________________
2. Выбираем интервалы ______штук по ______ мм.
3. Строим кривую зависимости числа измерений в каждом интервале (обычно получается типа 1 или 2)

График 1
Если кривая распределения имеет вид 1, то основная причина погрешностей – случайная.
Кривая 2, как правило, образуется в результате измерения микрометром, из-за систематической ошибки – 0,5 мм (ошибочное чтение показаний на стебле.) В этом случае надо перемерить размер штангенциркулем, выявить и пересчитать ошибочные значения и вычертить исправленную кривую на том же графике.
4. По графику устанавливаем наиболее вероятный действительный размер и сравниваем его с Хср; определяем наибольшую погрешность измерения и сравниваем ее с предельной погрешностью для этого средства измерения
Хср = _______________ Хнаиболее вероятный ≈ ___________________________
Наибольшая погрешность Хср - Xmin (max) __________________________________
Нормативная инструментальная погрешность =_______________
Допустимая погрешность при измерении этим СИ_____________
5. Диапазон разброса размеров делится на 3 равных части и подсчитывается, сколько результатов попало в центральную 1/3 и 2/3 интервала.
Все измерения попали в диапазон _____________________мм ______________100%
Центральная треть _____________________________ мм _____________________%
Центральные две трети__________________________мм ______________________%
Отбрасываем Хmax и Xmin и заново рассчитываем Хср = _________ и Хmax – Xmin =__________
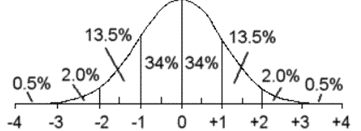
График 2
Сравниваем с нормальным: Сколько % измерений попали в нормативную погрешность?
6. Анализ результатов и выводы
Надо ответить на вопросы:
- Сколько процентов измерений (без явных грубых ошибок) попали в допустимую погрешность?
- Какова доля погрешности СИ в общей?
- Можно ли утверждать, что погрешность СИ непременно обеспечит большую точность измерения? Какие причины систематических погрешностей выявлены?
- Можно ли утверждать, что однократное измерение достоверно?
- Как можно уменьшить влияние систематических погрешностей на достоверность результата?
- Как можно снизить влияние случайных погрешностей?
- Ваши предложения по повышению точности и достоверности измерений вами (в рабочих условиях).
В результате совместно формируем алгоритм действий:
|
Систематическая погрешность |
Случайная погрешность |
Как проявляется при измерениях? |
|
|
Причины? |
|
|
Как можно обнаружить? |
|
|
Как можно уменьшить влияние погрешностей на результат? |
|
|