Не понимаю,что такое с людьми:
они учатся не через понимание,
а каким-то другим способом –
механическим запоминанием.
Из-за этого их знания очень шатки.
Р.Фейнман
Результат проверки заданий с развёрнутым ответом на ЕГЭ позволяет выявить главную проблему современного подхода большинства учителей в обучении физике. Это системное натаскивание учащихся на запоминание основных формул и математические преобразования с ними. Но ведь роль физики сформировать представление целостной картины мира и глубокое понимание фундаментальных законов природы. Показателем насколько успешно усвоен материал должно является умение решать задачи, требующие рассуждения. Число действительно основных законов природы исключительно мало. Кроме того эти законы формулируются довольно просто математически. После усвоения этих основных законов весь остальной материал без особого труда встаёт на своё место.
Одними из таких, являются законы Ньютона. На страницах учебников не уделяют должного внимания формированию физической сущности данных законов, поверхностно и формально вводят такие понятия как масса, сила, импульс, время, пространство. Оставим классическое изложение из учебников и рассмотрим несколько другой подход в изучении законов Ньютона. Но для этого отметим, что среди законов природы существуют основные к которым в первую очередь относятся законы сохранения. В механике это законы сохранения импульса и энергии. Следовательно понятие импульса и энергии являются основополагающими для понимания законов природы.
Начнём со второго закона Ньютона. Первоначальная формулировка Ньютона отличается от приведённых в учебниках.
Изменение количества движения(импульса) пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.
Количество движения (импульс) понятие введённое Ньютоном как характеристика тела p=m·ʋ. Напомним, что эта формулировка справедлива при движении со скоростями меньше скорости света. При больших скоростях масса зависит от скорости
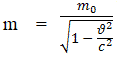
Приложенная сила в трактовке Ньютона есть действие, производимое над телом, чтобы изменить его состояние покоя или равномерного прямолинейного движения. Математически второй закон Ньютона в первоначальной трактовке имеет следующий вид:
![]()
Ньютон утверждал, что сила, действующая на тело равна скорости изменения импульса тела за малый промежуток времени. Если считать массу тела постоянной, то
![]()
Т.е движение тела не является доказательством действия силы. Если нет изменения скорости или изменения траектории => нет силы (равнодействующей) => тело находится в состоянии покоя или равномерного прямолинейного движения.
Исходя из этих рассуждений видно, что первый закон Ньютона это частный математический случай более общего второго закона. Всякое тело продолжает удерживаться в состоянии покоя или равномерного прямолинейного движения пока и поскольку оно не понуждается к этому приложенными силами изменить это состояние. Одна из причин, по которой этот частный случай выделен в отдельный закон - это его противоречие повседневным наблюдениям. Раскрытие первого закона Ньютона в школе представляет для учителя трудности. Известно, что если перестать тянуть или толкать движущееся тело, то оно как правило остановится, а не будет продолжать двигаться с постоянной скоростью. До Ньютона в науке господствовало учение Аристотеля, который считал, что для приведения тела в движение и для сохранения этого движения всякое тело - как земное, так и небесное - нуждается в двигателе. Движущая причина, или сила, необходима, чтобы тело могло двигаться.
Говоря о законах природы необходимо указывать границы их применимости Ньютон указал что все его законы справедливы, если наблюдатель находится в так называемой инерциальной системе отсчёта, которая покоится или движется прямолинейно и равномерно по отношению к неподвижным звёздам. И нарушаются, если наблюдатель движется сам с ускорением или движение происходит со скоростями близкими к скорости света.
Наиболее сложным для изучения является третий закон. Действию есть всегда равное и противоположное противодействие – иначе, взаимодействие двух тел друг на друга между собою равны и направлены в противоположные стороны. При изучении этого закона подчеркивают, что действие тел носит взаимный характер. В третьем законе в отличие от второго в равной степени рассматривают оба тела. Термины «действие» и «противодействие» – условны и взаимозаменяемы. При взаимодействии двух тел действие первого тела на второе можно назвать «действием» (F12), а второго на первое «противодействием» (F21), и наоборот. Важно довести до понимания учащихся тот факт, что эти силы нельзя складывать и не следует их путать с уравновешенными силами. (Уравновешенные силы приложены к одному телу, силы «действия» и «противодействия» – к разным телам: точки их приложения не следует (нельзя!) совмещать.)
Недопустимо толкование этих терминов как первичного (причины) – «действия» и как вторичного (следствия) – «противодействия». Третий закон Ньютона не является абсолютно справедливым. Например его нельзя применять к силе, действующей на расстоянии. Приведём простой пример: заряженная частица удаляется от проводника, по которому течёт электрический ток. На частицу в соответствие с законами электродинамики действует сила. В тоже время результирующая сила, действующая на проводник с током равна нулю. Это явно противоречит третьему закону, утверждающему, что действия тел друг на друга равны по величине. Но именно благодаря третьему закону гравитация не могла рассматриваться как некое изолированное свойство присущее центральному телу Солнечной системы. Она должна быть присуща и Луне, каждой планете, комете и звезде во Вселенной – мысль вероятно одна из величайших когда-либо приходивших человеческому уму.
Следует отметить, что к моменту издания в 1687 году «Математических начал натуральной философии» не существовало понятие векторных и скалярных величин. Без понятия «вектор» невозможно изучение механики, электростатики, электродинамики, магнетизма. Недаром векторное исчисление получило современный вид благодаря работам физиков (Гиббс Джозайя Уиллард).
Подавляющая часть учащихся испытывают затруднения, выполняя действия по преобразованию векторных уравнений. Поэтому важным условием успешного преподавания физики является обязательное предварительное изучение основ векторной алгебры. Учитель физики должен в совершенстве сам владеть этими основами, согласовывать свои методы изложения с учителем математики и школьной программой геометрии. Это позволит в дальнейшем избежать типичных ошибок при введении понятия вектор на уроках физики.
После чёткого введения понятий векторных и скалярных величин, необходимых для описания физических процессов, следует показать учащимся преимущество векторной записи уравнений. Векторная запись всегда короче и не зависит от выбора системы отсчёта и сохраняется при переходе из одной системы отсчёта в другую.
При этом надо помнить, что физика – наука экспериментальная и должна опираться на результаты опыта. Почему сила – векторная величина? Следует объяснять, опыт показывает что сила характеризуется числовым значением, направлением и может складываться с другой силой геометрически.
Следовательно, сила – векторная величина. Но чаще на уроках определение силы даётся наоборот. Или из формулы ![]() следует, что вектор ускорения совпадает с направлением равнодействующей приложенных сил. Не опираясь на знания из геометрии правил умножения вектора на число нельзя дать учащимся понимания роли абстрактных математических понятий и формул в реальном воплощении физических процессов и обеспечить осознание единства материального мира.
следует, что вектор ускорения совпадает с направлением равнодействующей приложенных сил. Не опираясь на знания из геометрии правил умножения вектора на число нельзя дать учащимся понимания роли абстрактных математических понятий и формул в реальном воплощении физических процессов и обеспечить осознание единства материального мира.
Со времен Ньютоновских начал они претерпели значительные изменения и дополнения, установлены границы применения. Но до сих пор они являются основой современной научной картины мира и служат основой для развития многих современных технологий. Невозможно сформировать единую целостную картину мира без понимания законов Ньютона.
Литература
- Лернер Я.Ф. Векторные величины в курсе механики средней школы. Физика в школе. 1971. №2 с.36-39.
- Перышкин А.В. Физика. 9 класс [Текст]: учебник для общеобразовательных учреждений. / А.В. Перышкин, Е.М. Гутник. – М.: Дрофа, 2014. - 319с.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия: учебник для общеобразовательных учреждений - 22-е издание. М. Просвещение, 2012. 384с.
- http://mathus.ru/phys/vectors.pdf.
- Ньютон Исаак. Математические начала натуральной философии. М.: Наука, 1989.
- Орир Дж.Популярная физика. М. Мир, 1966.