Предисловие
Уравнения занимают значительное место в курсе математики средней школы. Остановимся лишь на алгебраических уравнениях, которые разобьем на три группы:
- полиномиальные уравнения вида Pn(x) = 0, где Pn(x) — многочлен n-й степени относительно x;
- дробно-рациональные уравнения, т.е. содержащие в качестве двух компонент частные двух многочленов;
- иррациональные уравнения.
Для ряда приемов даны небольшие теоретические обоснования. Приведено 30 приемов, иллюстрированных более чем 36 примерами. Не надо думать, что приведенный в конкретном примере прием является наиболее рациональным для решения данного примера. Просто надо принять к сведению существование такого подхода к решению уравнений.
Одни и те же подходы (применение тригонометрии, использование однородности, разложение на множители и др.) находят применение не только при решении рациональных, дробно-рациональных, иррациональных уравнений, но и при решении трансцендентных уравнений, неравенств, систем.
При написании использовалась литература:
- Рывкин А. А. «Справочник по математике» – М.: Высшая школа, 1987.
- Цыпкин А. Г. «Справочник по методам решения задач по математике» – М.: Наука, 1989.
- Шарыгин И. Ф. Факультативный курс по математике – М.: Просвещение, 1989.
- Сборник задач по математике для поступающих во ВТУЗы / Под ред. Сканави М. И. – Мн.: Вышэйшая школы, 1990.
и др.
В этих пособиях можно найти достаточное количество нужных уравнений, конечно, не пренебрегая другими источниками.
Полиномиальные уравнения
1. Докажем теорему: Если уравнение anxn + an–1xn–1 + … + a1x + a0 = 0 (*) с целыми коэффициентами имеет рациональный корень, где p и q взаимно просты, то a0 делится на p, а an делится на q.
Доказательство: Заменим в (*) x на , получим верное числовое равенство умножим обе части равенства на qn:
anpn + an–1pn–1q + … + a1pqn–1 + a0qn = 0 (**)
anpn = – q (an–1pn–1 + … + a1pqn–2 + a0qn–1)
Правая часть делится на q, значит, и левая должна делиться на q, но т.к. p и q взаимно просты, то pn не делится на q, но тогда an должно делиться на q, иначе левая часть не будет кратна q.
Из (**) можно получить и другое равенство a0qn = – p (anpn–1 + an–1pn–2q + … + a1qn–1)
Правая часть кратна p, значит, и левая кратна p, но qn взаимно просты с p, значит a0 кратно p. Теорема доказана.
Теорема Безу. Остаток от деления многочлена P(x) = anxn + an–1xn–1 + … + a1x + a0 на двучлен (x – a) равен значению многочлена P(x) при x = a.
Доказательство: Делимое равно делителю, умноженному на частное, плюс остаток. Так как делитель — многочлен первой степени, то остаток будет многочленом, степень которого меньше степени делителя, значит, остаток – const. Частное будет многочленом степени n – 1. Тогда
P(x) = (x – a) (сn–1xn–1 + сn–2xn–2 + … + с1x + с0) + R (***)
При x = a это равенство имеет вид
P(a) = 0 ? (сn–1an–1 + сn–2an–2 + … + с1a + с0) + R,
из которого следует P(a) = R. Теорема доказана.
Следствие: Если x = a — корень многочлена, то многочлен делится на x – a без остатка.
Доказательство: При x = a равенство (***) примет вид 0 = 0 + R, из которого следует, что R = 0. А так как остаток от деления равен нулю, то утверждение доказано.
Пример 1. Решить уравнение 30x4 + x3 – 30x2 + 3x + 4 = 0.
Составим различные несократимые дроби, числители которых — делители свободного члена, т.е. 4, а знаменатели — делители старшего коэффициента, т.е. 30.
В левом столбике в знаменателях участвуют все делители числа 30. Видно, что – 1 — корень многочлена. По следствию из теоремы Безу делим многочлен на x + 1
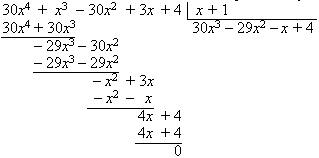
Для поиска корней многочлена 30x3 – 29x2 – x + 4
воспользуемся таблицей дробей. При 
многочлен
примет вид 
Значит, 
— корень многочлена.
2. При решении алгебраических уравнений может быть полезен метод неопределенных коэффициентов.
Пример 2. Решить уравнение x4 + 2x3 – 16x2 + 11x – 2 = 0.
Пусть многочлен представим в виде произведения
(a x2 + b x + g ) (ax2 + bx + c),
где a , b , g , a, b, c коэффициенты, которые желательно подобрать так, чтобы после раскрытия скобок и приведения подобных слагаемых получился исходный многочлен. Раскроем скобки, полагая, что a = a = 1.
(x2 + b x + g ) (x2 + bx + c) = x4 + (b + b)x3 + (b b + g +c)x2 + (g b + b c)x + cg
Приравняем коэффициенты
b + b = 2 b = 2 – b
b b + g +c = – 16 2b – b2 + g +c = – 16
g b + b c = 11 g b + 2c – bc = 11
cg = – 2 cg = – 2
Положим c = 1, g = – 2 или c = 2, g = – 1 (подбираем коэффициенты).
– 2b – b = 9
b = – 3, тогда b = 5.
Убедимся, что b = 5, g = – 2, b = – 3, c = 1. Такой набор удовлетворяет всем четырем уравнениям, поэтому можем записать
x4 + 2x3 – 16x2 + 11x – 2 = (x2 – 3x + 1) (x2 + 5x – 2)
Решив квадратные уравнения, получим корни исходного уравнения.
Ответ: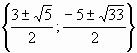 
3. Решение возвратных уравнений
Уравнения вида ax2k + bx2k–1 + cx2k–2 + … + l k–2cx2 + l k–1bx + l a = 0 (k I N, l I R) называются возвратными.
После почленного деления на xk, они решаются подстановкой
Пример 3. Решить уравнение 2x4 – 3x3 – 7x2 –15x + 50 = 0.
Разделим на x2, получим 
Уравнение примет вид:
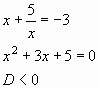
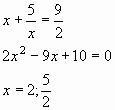
Если l = 1, то уравнение вида ax2k + bx2k–1 + cx2k–2 + dx2k–3 + … + dx3 + cx2 + bx + a = 0 называется возвратным (или симметрическим) уравнением степени 2k первого рода.
Пример 4. Решить уравнение 5x4 + 3x3 – 16x2 + 3x + 5 = 0.
Разделим почленно на x2. Имеем 
.
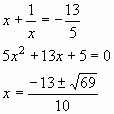
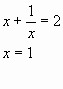
Ответ: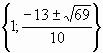 
Если l = – 1, то получим уравнение вида
ax2k + bx2k–1 + cx2k–2 + dx2k–3 + … + dx3 + cx2 – bx + a = 0, которое называется возвратным (или симметрическим) уравнением степени 2k второго рода. Решается подстановкой
Пример 5. Решить уравнение 8x4 – 42x3 + 29x2 + 42x + 8 = 0.
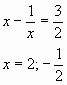
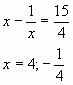
Ответ: 
Возвратное уравнение нечетной степени имеет корень – 1. Это объясняется тем, что уравнение имеет четное число членов, которые при замене x на – 1 попарно уничтожаются. Поэтому в начале делят многочлен на x + 1, а частное приведет к возвратному уравнению четной степени, решение которого уже рассмотрено.
Пример 6. Решить уравнение 24x5 + 74x4 – 123x3 – 123x2 + 74x + 24 = 0.
Имеем возвратное уравнение 5-й степени. Один из его корней – 1. После деления на x + 1, получим
24x4 + 50x3 – 173x2 + 50x + 24 = 0
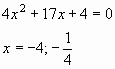
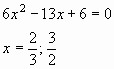
Ответ: 
если 
,
то 
По биному Ньютона
Замечание 2. Определить по внешнему виду, что
уравнение является возвратным не всегда просто,
особенно, если 
. Поэтому в уравнении степени 2n
производим почленное деление на xn и,
если при этом получается сумма выражений вида ,
где n = 0, 1, 2 … m, то
дальнейшее решение ясно.