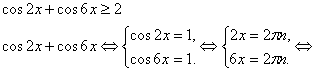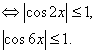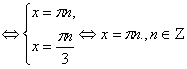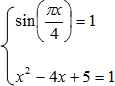Цель: Расширение знаний в решения нестандартных задач.
Задачи:
- уметь анализировать ситуации, замечать существенное, выявлять общее и делать выводы, переносить известные приемы в нестандартные ситуации, находить пути их решения;
- самостоятельно выдвигать гипотезы, логически обосновывать суждения, точно и грамотно выражать свои мысли в устной и письменной речи, принимать решения.
- Развивать логическое и математическое мышление, развивать письменную и речевую математическую культуру учащихся.
Тип урока: урок совершенствования знаний, умений и навыков.
Метод работы: частично–поисковый, репродуктивный.
Дидактический материал: раздаточный материал для каждого обучающегося, анкеты.
План урока:
- Организационный момент.
- Проверка домашнего задания.
- Домашнее задание.
- Решение нестандартных задач.
- Итог урока.
Ход урока
I. Организационный момент.
Вступительное слово учителя. Обучающимся объявляется тема урока, цели и план урока.
II. Проверка домашнего задания.
Работа в парах. Взаимопроверка. На дом были заданы уравнения. В таблице ставят + и –.
Критерий оценок:
- 5 или 6 уравнений – «5»
- 4 уравнений – «4»
- 3 уравнений – «3»
- Менее 3 уравнений – «2».
Решить уравнения:
-
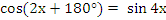
Ответ: –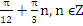 , –
, – 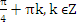
-
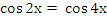
Ответ: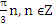 ,
, 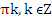
-
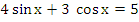
Ответ: ,
, -
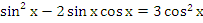
Ответ: –
-
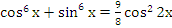
Ответ: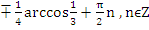
-
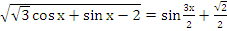
Ответ: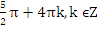
| 1 задание | 2 задание | 3 задание | 4 задание | 5 задание | 6 задание |
III. Домашнее задание.
Задания 1 и 2 уровней на «3»
Задания 2 и 3 уровней на «4»
Задания 3 и 4 уровней на «5»
ЗАДАНИЯ 1 УРОВНЯ
№1 Какие из данных уравнений не имеют корней?
а) sinх = –0,02;
б) cosх = –1,01;
в) tgx = 0;
г) sinx =;
д) sinx = 102/101;
е) tgx = π
ж) cosx =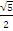
№2. Решите уравнения:
а) tgx = –1;
б) 2 cosx+1 = 0;
в) 2sin2x+sinx = 0;
г) ctg2x = 1;
д) 3cos2x–4sinx cosx+sin2x = 0;
е) cosx+cos3x=0;
ж) 2cos2x+5sinx – 4 = 0.
№3 Решите неравенство:
а) sinx
;
б) cosx; ;
в) 2cosx – 1;
г) tgx < –1.
ЗАДАНИЯ 2 УРОВНЯ
№1 Для каких из данных уравнений число π является корнем уравнения?
а) 2sinx = 0;
б) 3cosx = 0;
в) sinx = cosx;
г).
№2 Решить уравнение:
а) sin (π – x) + cos (
+x) = 0;
б) sin 7x – sin 3x – cos 5x = 0;
в) 2sin3 – cos 2x – sin x = 0.
№3 Изобразив схематически графики, определите, сколько корней имеет уравнение: сos x = 2x
№4 Найти корни уравнения:
а) sinx =
на
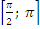
б) cos x = –на [0; π].
ЗАДАНИЯ 3 УРОВНЯ
№1. Составьте тригонометрическое уравнение вида sinx = a, решения которого включает точки, отмеченные на единичной окружности.
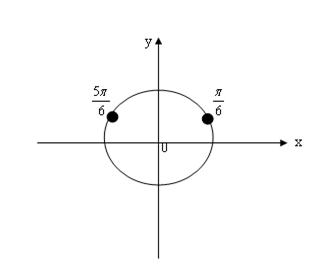
№2 Решите уравнение:
а) 1– cos 6x = tg 3x;
б) sin x + 2 cos x =.
№3. Решите систему:
№4 Решите неравенство:
а)
>
;
б)<.
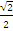
ЗАДАНИЯ 4 УРОВНЯ.
Решите уравнение:
-
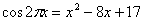
-
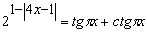
-
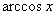 =
= 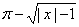
-
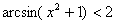
-
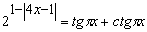
-
Решить уравнение
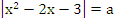 в зависимости от параметра а.
в зависимости от параметра а. -
При каких значениях параметра а имеет корни уравнение
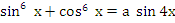
IV. Решение нестандартных задач
Решить уравнения и системы уравнений:
-
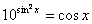
-
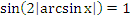
-
12
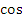 3x+
3x+ 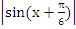 ≥13
≥13 -
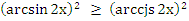
-
16
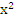 –40 x +31 = (
–40 x +31 = (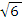 –
– 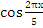 ) (
) (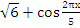 ). Если уравнение имеет более одного корня, то в бланке ответов запишите сумму всех его корней (из ЕГЭ 2008).
). Если уравнение имеет более одного корня, то в бланке ответов запишите сумму всех его корней (из ЕГЭ 2008). -
Найти все значения параметра а, при которых система уравнений имеет единственное решение
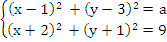
-
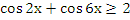
-

Понятие нестандартных задач и нестандартных методов решения. Классификация нестандартных методов решения: метод мажорант, метод монотонности, метод тригонометрической подстановки, применение производной, геометрический подход, применение области определения функций. Привести пример из заданий ЕГЭ по математике:
Детей рассадить парами (сильного и слабого) с целью взаимопомощи,
Метод мажорант (метод оценки ограниченности функций)
Понятие метода мажорант и основной идеи этого метода. Рассматривается метод, когда на общей части областей существования функций, находящихся в левой и правой части, каждая из них ограничена слева или справа одним и тем же числом.
Пусть мы имеем уравнение ![]() и существует число М, такое, что для любого x из области определения
и существует число М, такое, что для любого x из области определения ![]() и
и ![]()
![]() и
и ![]() . Тогда уравнение
. Тогда уравнение ![]() ,
, ![]() Число M называется мажорантой.
Число M называется мажорантой.
Пример 1: Решить уравнение:
Оценим: ![]()

Правая часть: ![]()
![]()
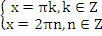
– решение системы, а значит, исходного уравнения.
Ответ: x= 2![]()
Пример 2: ![]()
Решение: Преобразуем исходное уравнение (везде k![]() Z):
Z):
Поскольку
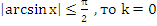
Осталось решить уравнение: ![]()
Ответ: ![]()
Пример 3: 12 cos 3x+ ![]() ≥13
≥13
Решение: Т.к. ![]() ,
, ![]() , то данное неравенство может быть верно, только если одновременно
, то данное неравенство может быть верно, только если одновременно ![]()
![]()
![]()
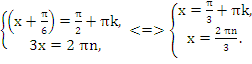
Везде n, k ![]() . Решение последней системы может быть получено на тригонометрическом круге. Действительно, первое неравенство задаёт точки
. Решение последней системы может быть получено на тригонометрическом круге. Действительно, первое неравенство задаёт точки ![]() и
и ![]() , а второе неравенство – точки
, а второе неравенство – точки ![]() ,
, ![]() и
и ![]() Общее решение:
Общее решение: ![]() (или –
(или – ![]() )
)
Ответ: x= – ![]() +
+ ![]() Z
Z
Пример 4: ![]()
Решение: Преобразуем неравенство: ![]()
Воспользуемся равенством ![]()
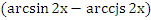
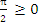
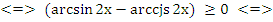
Поскольку функция у=
– возрастает, то последнее неравенство равносильно
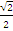
откуда и получим ответ:
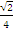
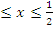
Пример 5: 16 ![]() –40 x +31 = (
–40 x +31 = (![]() –
– ![]() ) (
) (![]() ). Если уравнение имеет более одного корня, то в бланке ответов запишите сумму всех его корней (из ЕГЭ 2008).
). Если уравнение имеет более одного корня, то в бланке ответов запишите сумму всех его корней (из ЕГЭ 2008).
Решение: В левой части уравнения –квадратичная функция. Выделим полный квадрат:
y=
. Теперь понятно. Что множество её значений– отрезок
.
В правой части уравнения– функция y=6 –
. Множество её значений– отрезок
. Значит, решением уравнения 16
–40 x +31 = (
–
) (
) являются те, и только те значения переменной, при которых значения и левой и правой частей равны числу 6. Квадратичная функция y= 16
–40 x +31 принимает значение у=6 только при х=
. Найдём значение функции у=(
–
) (
) при полученном значении х: у(
)= 6 –
= 6 –
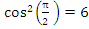
Ответ: х=![]() – единственный корень уравнения.
– единственный корень уравнения.
Геометрическое решение алгебраических задач (геометрические интерпретации).
Геометрические интерпретации (иллюстрации) удобны и доступны для понимания подавляющего большинства учащихся, так как с их использованием алгебраическая задача перестаёт быть абстрактной и отвлечённой, а найденные решения в процессе их поиска становятся частью опыта учащегося. Геометрический образ откладывается в сознании и легко может быть актуализирован в аналогичной или даже незнакомой ситуации. Таким образом, формируется геометрическое мышление, т. е. развивается умение оперировать различными геометрическими объектами, интерпретировать алгебраические задачи геометрически. Это позволяет решать такие задачи, которые алгебраическими методами решать весьма затруднительно, если вообще возможно.
Пример 6 . Найти все значения параметра а, при которых система уравнений имеет единственное решение ![]()
Решение: На языке геометрии задание означает, что требуется найти все значения параметра а, при каждом из которых окружность с центром в точке (1; 3) и радиусом ![]() касается окружности с центром в точке (–2; –1) и радиусом 3, При внешнем касании это означает что
касается окружности с центром в точке (–2; –1) и радиусом 3, При внешнем касании это означает что ![]() +3 =5; при внутреннем касании, что
+3 =5; при внутреннем касании, что ![]() –3= 5 ( число 5 – расстояние между центрами окружностей). Сделать рисунок к задаче.
–3= 5 ( число 5 – расстояние между центрами окружностей). Сделать рисунок к задаче.
Ответ: 4 и 64
Пример 7: Решить неравенство:
Пример 8. Решить уравнение: ![]()
Рассмотрим функции: ![]()
E(f) = [–1; 1]
E(g) = [1; +∞]E(f)
= { 1 }Отсюда: данное уравнение равносильно системе:
Решим I уравнение системы: ![]()
n
Z
, n
Z
, n
Z
Решим II уравнение системы: ![]()
Отсюда: решением системы, а значит и данного уравнения является x = 2
Ответ: 2.
Ответ: ![]()
Ответ: 4 и 64
V. Итог урока.
Провести анкетирование:
Анкета Ф.И. _______________________________________
- Нуждаешься ли ты в индивидуальной консультации?
Да ______ Нет ______ - Затрудняюсь:
А) при решении простейших тригонометрических уравнений: ______
Б) при решении простейших тригонометрических неравенств: ______
В) при решении систем тригонометрических неравенств: ______
Г) при решении однородных тригонометрических уравнений: ______
Д) при решении тригонометрических уравнений методом разложения на множители: ______
Е) при решении тригонометрических уравнений, приводимых к алгебраическим методам подстановки: ______
Ж) при решении тригонометрических уравнений методом введения вспомогательного угла: ______
З) при решении тригонометрических уравнений методом понижения степени: ______
И) при решении тригонометрических уравнений с параметрами: ______
К) при решении уравнений с обратными тригонометрическими функциями: ______
Литература:
- П.В. Чулков Лекции по программе курса Уравнения и неравенства в школьном курсе математики, – Москва: Педагогический университет «Первое сентября», 2009.
- Тимофеев Г.Н. Математика для поступающих в ВУЗы, – Йошкар-Ола, 2002.
- Олехник С.Н. Нестандартные методы решения уравнений и неравенств: Справочник / С.Н. Олехник, М.К. Потапов, П.И. Пасиченко. – М.: Изд–во МГУ, 1991. – С. 143.
- Б.М. Ивлев, А.М.Абрамов, Ю.П. Дудницин, С.И. Шварцбурд Задачи повышенной трудности по алгебре и началам анализа для учащихся 10–11 классов средней школы М.: Просвещение, 1976. – С. 47.
- Денищева Л.О., Карюхина Н.В., Михеева Т.Ф. "Учимся решать ур-я и нер-ва", 10–11 кл.; – М.: Интеллект-центр, 2002.
- С.М. Никольский, М.К. Потапов и др. "Алгебра и начала анализа", учебник для 11 кл. общеобразовательных учреждений, – М.: "Просвещение", 2006.
- Сборник задач по математике для поступающих в ВУЗы, алгебра. Под редакцией М. И. Сканави, – М.: ОНИКС, 21 век, 2002.
- Л.О. Денищева, Глазков Ю.А. и др."ЕГЭ-2007", Математика, – М.: изд-во Интеллект-центр, 2007.