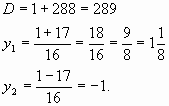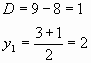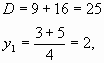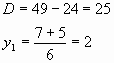Цель: научить решать тригонометрические уравнения.
Задачи:
- учить решать тригонометрические уравнения;
- развивать интеллектуальную культуру учащихся;
- воспитывать аккуратность, точность, интерес к предмету.
Тип урока: комбинированный
Оснащение учебного процесса: мультимедийный проектор, компьютер, карточки – задания.
Ход занятия
1. Организационный момент.
2. Актуализация опорных знаний:
а) формула корней уравнения sin ![]() где
где ![]()
![]()
Ответ:
, где
б) формула корней уравнения cos ![]() где
где ![]()
![]()
Ответ:
, где
в) формула корней уравнения tg ![]() где
где ![]() – любое число
– любое число
Ответ:
, где
Решите уравнения:
1) sin
Решение:
,
,
, где
Ответ: ![]() ,
где
,
где ![]()
2) cos![]()
Решение:
где
Ответ: ![]() где
где ![]()
3) tg ![]()
![]()
Решение:
, откуда
, а
, где
.
Ответ: ![]() ,
где
,
где ![]() .
.
3. Изложение нового материала:
Более сложные тригонометрические уравнения, как, правило, сводятся к простейшим уравнениям.
1) Метод разложения на множители.
Пример 1. Решить уравнение ![]() .
.
Решение: Вынесем общий множитель за скобки и
получим ![]() .
.
Рассмотрим случаи:
а) cos
, тогда
, где
.
б)
, тогда cos
,
, где
.
Ответ: ![]() ,
, ![]() , где
, где ![]() .
.
2) Метод замены переменных.
Пример 2. Решить уравнение ![]()
Решение:
,
,
,
.
Заметим, что данное уравнение представляет
собой квадратное уравнение относительно ![]() . Обозначим
. Обозначим ![]() , получим
квадратное уравнение
, получим
квадратное уравнение
Получаем два случая:
1) ![]() . В этом
случае нет корней, т.к.
. В этом
случае нет корней, т.к. ![]() .
.
1) ![]() , откуда
, откуда ![]() , где
, где ![]() .
.
Ответ:
, где
.
Методом замены переменных можно решать и однородные тригонометрические уравнения.
Тригонометрическое уравнение называют однородными, если после некоторой замены полученный многочлен от двух переменных составлен из одночленов одинаковой степени.
Пример 3. Решить уравнение ![]() .
.
Решение. Рассмотрим два случая:
1) ![]() , тогда
, тогда ![]() , откуда
, откуда ![]() , что
невозможно, т.к.
, что
невозможно, т.к. ![]() ; в этом случае корней нет.
; в этом случае корней нет.
2) ![]() , тогда
разделим обе части уравнения на
, тогда
разделим обе части уравнения на ![]() :
:
Пусть ![]() .
Получим уравнение
.
Получим уравнение ![]()
, откуда
, где
, откуда
, где
.
Ответ:
,
, где
.
При решении тригонометрических уравнений можно использовать и так называемую универсальную тригонометрическую подстановку на основе формул:
,
,
.
Пример 4. Решить уравнение ![]()
Решение:
Сделаем универсальную подстановку ![]() , тогда
, тогда ![]() , отсюда
, отсюда ![]() ,
, ![]() , тогда
, тогда ![]() или
или ![]()
![]()
![]() .
.
Таким образом:
а)
, откуда
,
, где
.
б)
, откуда
,
, где
.
Ответ:
,
, где
.
3) Закрепление изученного материала.
Пример 1. Решить уравнение ![]()
Решение:
,
Обозначим ![]() ,
получим уравнение
,
получим уравнение
Таким образом:
а)
. В этом случае нет корней, т.к.
б)
, откуда
, где
.
Ответ:
, где
.
Пример 2. Решить уравнение ![]()
Решение:
Рассмотрим два случая:
1) ![]() , тогда
, тогда ![]() , откуда
, откуда ![]() , что
невозможно, т.к.
, что
невозможно, т.к. ![]() ; в этом случае корней нет.
; в этом случае корней нет.
2) ![]() , тогда
разделим обе части уравнения на
, тогда
разделим обе части уравнения на ![]() :
:
Пусть ![]() .
Получим уравнение
.
Получим уравнение ![]()
Таким образом:
а)
, откуда
, где
б)
, откуда
, где
.
Ответ:
,
, где
.
4. Предлагается самостоятельная работа.
Самостоятельная работа
Вариант 1
Решить уравнения:
1)
2)
3)
Самостоятельная работа
Вариант 2
Решить уравнения:
1)
2)
3)
Самостоятельная работа
Вариант 3
Решить уравнения:
1)
2)
3)
5. Итог занятия.
6. Домашнее задание.