Предлагаемые при итоговой аттестации учащихся задания группы С5 интересны для учителей и выпускников не только с точки зрения достижения результата на экзамене, но и как средство сравнения возможностей реализуемой учителем образовательной программы для разных групп учащихся. Рассмотрим задание С5, предлагавшееся в 2013 для выпускников 11 класса, решение одним способом аналога которого приведено в книге С.А. Шестакова «ЕГЭ 2014. Математика Задача С5 Задачи с параметром» издательства МЦНМО на стр. 156 -157 .
С5. Найдите все значения а, при каждом из
которых уравнение ![]() имеет единственный корень.
имеет единственный корень.
Данное задание можно решать с помощью приемов, доступных выпускникам 9 классов.
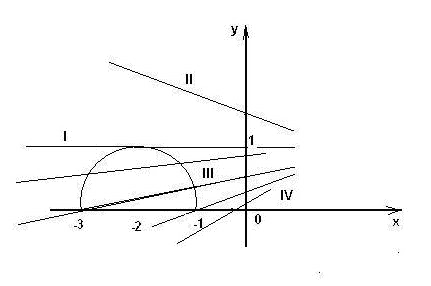
Рисунок 1
Способ 1
. Использование графической интерпретации. Перепишем уравнение в видеСледовательно, единственное решение у уравнения будет в случае а = 0 или для а из [– 1/4; – 1/6).
Ответ: ![]() .
.
Способ 2. Более интересной будет
графическая иллюстрация, если заметить, что
задаваемое семейство прямых представляет собой
пучок прямых. Все прямые, кроме вертикальной,
проходящие через точку (х0;у0) могут быть заданы в
виде y – y0 = a (x –
x0), где ![]()
Для задания прямых используем преобразование y –
1 = a (x – 3), откуда получаем общую
точку всех прямых (3; 1). Решение задачи может
сопровождаться рисунком, приведенным ниже, где
обозначение граничных положений такое же, как и в
способе 1. Однако, на экзамене выпускник
самостоятельно не придет к понятию пучка прямых,
если соответствующая конструкция не будет
отработана с учащимися при подготовке к
экзамену. Ответ в задаче получается аналогичными
способу 1 расчетами.
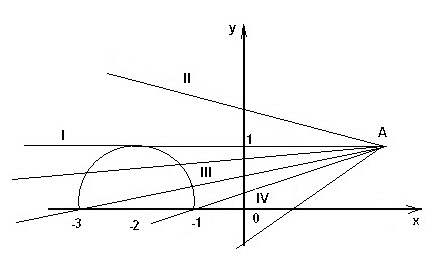
Рисунок 2
Способ 3. Для данной задачи возможно
получить вполне корректное решение, если
даже не увидеть уравнения полуокружности,
а привести исходное уравнение к виду,
позволяющему проанализировать взаимное
положение графика функции ![]() и семейства прямых g(x)
= a(3 – x). Область определения f(x)
– отрезок [–3;–1], причем на [–3;–2] f(x)
возрастает, на [–2;–1] – убывает. Множество
значений функции f(x) – отрезок [–1;0].
Пучок прямых, задаваемый g(x), проходит
через точку (3;0). Наличие общих точек
анализируется похожим образом на способ 2, не
используя явного вида графика f(x).
и семейства прямых g(x)
= a(3 – x). Область определения f(x)
– отрезок [–3;–1], причем на [–3;–2] f(x)
возрастает, на [–2;–1] – убывает. Множество
значений функции f(x) – отрезок [–1;0].
Пучок прямых, задаваемый g(x), проходит
через точку (3;0). Наличие общих точек
анализируется похожим образом на способ 2, не
используя явного вида графика f(x).
Способ 4. Равносильный переход с
последующим исследованием расположения корней
квадратного трехчлена.
Большая часть работ выпускников, авторы
которых идут по аналитическому пути решения
задачи, содержит только первый маленький шаг на
пути к верному решению.
![]()
Исследовав последнее квадратное относительно х уравнение, они делают ошибочный вывод, что наличие единственного корня данного уравнения обеспечивает выполнение условий исходной задачи.
В действительности исходное уравнение равносильно системе, в которую входит условие не отрицательности выражения, приравниваемого к радикалу.
![]()
Уравнение (1) приводится к виду 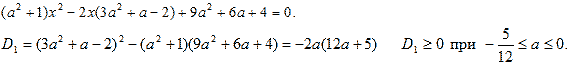
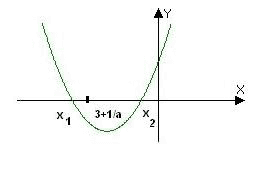
Рисунок 3
При а = 0 уравнение имеет единственный
корень х = –2. При a = –5/12 корень
уравнения (1)
x = –21/13 не удовлетворяет неравенству (2).
Учтем, что уравнение (1) имеет 2 корня при а <
0. Для х из неравенства (2) получаем x > 3 + 1/a
. Поскольку дискриминант квадратного трехчлена
уравнения (1) не представляет собой квадрат
простого выражения, достаточно проблематично
через иррациональные неравенства получить
значения параметра а. Задание существенно
упростится, если использовать метод составления
системы необходимых и достаточных условий,
соответствующей нужному расположению корней
квадратного трехчлена. Ветви соответствующей
параболы направлены вверх, меньший корень должен
лежать слева от значения 3 + 1/a, а больший –
справа. Уравнение (1) можно представить в виде f(x)
= 0, тогда требуемые значения параметра а будут
определяться из условия f(3 + 1/a) < 0 или
же x2 = 3 +1/а. Эти условия
являются и необходимыми, и достаточными. ![]() После
приведения к общему знаменателю и упрощения
получаем
После
приведения к общему знаменателю и упрощения
получаем ![]() При а
= – 1/4 получаем, что 3 + 1/а = –1 – больший
корень уравнения, при а = –1/6 получаем, что 3 +
1/а = –3 – меньший корень уравнения, что нас
не устраивает. Объединяя найденные значения а,
имеем
При а
= – 1/4 получаем, что 3 + 1/а = –1 – больший
корень уравнения, при а = –1/6 получаем, что 3 +
1/а = –3 – меньший корень уравнения, что нас
не устраивает. Объединяя найденные значения а,
имеем
Ответ: ![]()
Способ 5. Иррациональные неравенства.
К сожалению, если исследованию расположения корней квадратного трехчлена, почти не уделялось времени, то нам остается метод «тупо в лоб».
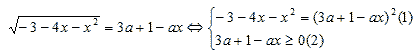
Уравнение (1) приводится к виду
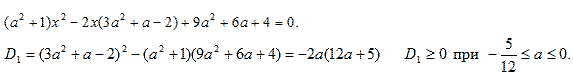
Как показано выше, из граничных значений имеем
а = 0. При D1 > 0 получаем ![]()
При а < 0 из (2)![]() и
и 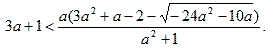
Система условий 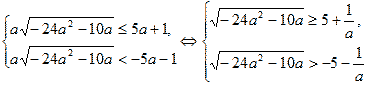 приводит
нас к равносильному при D1 > 0 (с
необходимостью учета строгого и нестрогого
неравенств системы) неравенству
приводит
нас к равносильному при D1 > 0 (с
необходимостью учета строгого и нестрогого
неравенств системы) неравенству
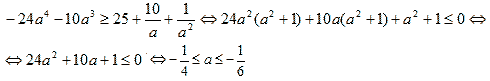
Учитывая замечания к способу 4, получаем
Ответ: ![]()
Способ 6. Применение элементов высшей
математики: f(x) = a.
В старшей школе много времени уделяется
элементам математического анализа, особенно в
классах с углубленным изучением математики.
Возможностью хоть как-то использовать
приобретенные навыки в этой области можно
воспользоваться и для решения задач группы С.
Исходное уравнение определено при ![]() На [– 3;– 1] перепишем
уравнение в виде
На [– 3;– 1] перепишем
уравнение в виде ![]() Пусть
Пусть
![]() D(f) = [–
3;– 1]. f(x) = 0 при x = – 2.
D(f) = [–
3;– 1]. f(x) = 0 при x = – 2.
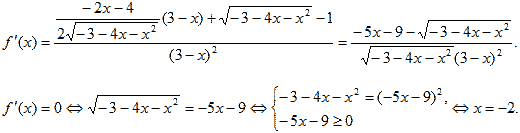
Определим множество значений функции. f(–3) = –1/6, f(–2) = 0, f(–1) = –1/4. Единственная точка экстремума на D(f) оказалась точкой максимума. Е (f) = [–1/4;0]. Построим эскиз графика функции y = f(x).
Как видно из представленного эскиза, уравнение f(x)
= a имеет единственное решение для ![]() .
.
Ответ: ![]()
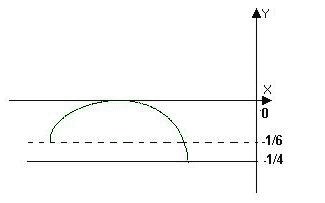
Рисунок 4.
Способ 7. Применение элементов высшей математики: f(x) = g(x).
Если мы смогли преобразовать исходное
уравнение к виду, когда одна из его частей не
зависит от параметра, то исследование числа
корней уравнения f(x) = a сводится к
определению числа точек пересечения графика f(x)
с горизонтальными прямыми. Правда, формулы для f(x)
громоздки. Однако, некоторый выигрыш в формулах
для задания функций, сполна компенсируется
поиском условий качания их графиков.
Исходное уравнение определено при ![]() На [– 3;– 1] перепишем
уравнение в виде
На [– 3;– 1] перепишем
уравнение в виде 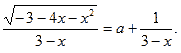 Построив
эскизы графиков левой и правой частей уравнения,
можно определить условие единственности корня
исходного уравнения. В способе 7 (в отличие от
способа 6) существует определенная проблема:
условие касания графиков при а = 0 следует
обосновывать.
Построив
эскизы графиков левой и правой частей уравнения,
можно определить условие единственности корня
исходного уравнения. В способе 7 (в отличие от
способа 6) существует определенная проблема:
условие касания графиков при а = 0 следует
обосновывать.
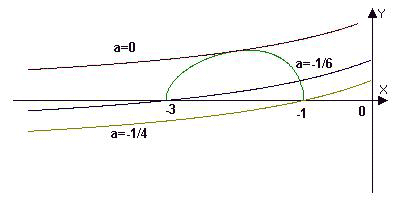
Рисунок 5.
Абсциссу точки касания графиков f(x) и g(x) найдем из условия равенства при этом аргументе значений функций и их производных.
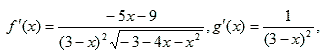
Получаем x0 = –2, а = 0. В качестве рекомендации, можно посоветовать ученикам стараться сводить использование графиков функций таким образом, чтобы с одной стороны появлялся график функции без параметра, а с другой стороны было выражение, зависящее только от параметра.