Элементы комбинаторики, относительно недавно снова войдя в школьный курс математики, принесли в него немало вопросов и трудностей.
Учащиеся в основном испытывают трудности при определении способа решения комбинаторных задач. Предлагаю ученикам выбирать решение задач с помощью таблицы (рисунок 1).
На уроках сначала провожу предварительную работу, опираясь на знания, полученные учащимися в 5 - 6 классах.
1. Выявляем две основные математические модели
- Модель 1: Размещение m шаров по n коробкам (размещение).
- Модель 2: В одну непрозрачную коробку помещены n шаров. Выбираются m шаров из n (выборка).
2. Определяем основные типы выборок и размещений.
Рассматриваем выборки:
а) упорядоченные (порядок расположения шаров учитывается, «важен»);
б) неупорядоченные (порядок расположения шаров не учитывается «неважен»).
Рассматриваем типы размещения шаров в коробки.
а) с повторением их в комбинации;
б) без повторения их в комбинации;
и типы выбора шаров:
а) с возвращением шаров в коробку (набор будет иметь повторяющиеся элементы);
б) без возвращения шаров в коробку ( набор не будет иметь повторяющиеся элементы).
3. Определяем виды шаров.
- Различимые.
- Неразличимые.
4. В соответствии с этими моделями рассматриваем основные способы нахождения количества комбинаций некоторых элементов различных множеств (формулы размещений, перестановок и сочетаний). Все эти факты выстраиваю в «Таблицу решения комбинаторных задач», с помощью которой обучающиеся определяют способ нахождения количества комбинаций. Механизм применения этой таблицы таков:
- Анализируя условие задачи, ребята определяют, какой из двух моделей оно соответствует (какое «действие» осуществляется с предметами: выбирают их, или размещают).
- В случае если необходимо найти количество комбинаций размещений, ученики находят в таблице «Число исходов размещения m шаров по n коробкам» (это верхняя часть таблицы). Затем ребята определяют тип предметов (шаров), различимы они или неразличимы и тип размещений (с повторением или без повторения). На пересечении выбранных
- столбца и строки учащиеся находят способ определения количества комбинаций.
- В случае, если необходимо найти количество комбинаций выбора предметов, ученики находят в таблице «Число исходов выбора m шаров из коробки с n шарами» (это нижняя часть таблицы). Затем ученики определяют тип выборки: упорядоченная (порядок выбора предметов «важен»), неупорядоченная (порядок выбора предметов «неважен»). А также определяется тип выбора: с возвращением или без возвращения. На пересечении выбранных столбца и строки ребята находят способ определения количества комбинаций выборки.
Решим задачи с помощью предложенной таблицы решения.
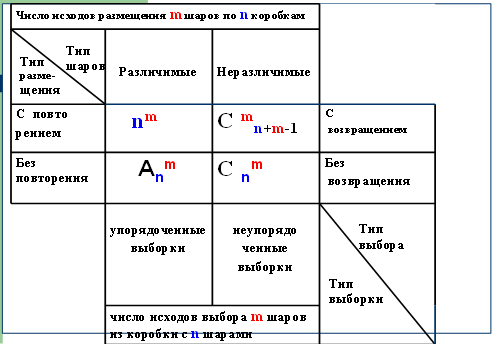
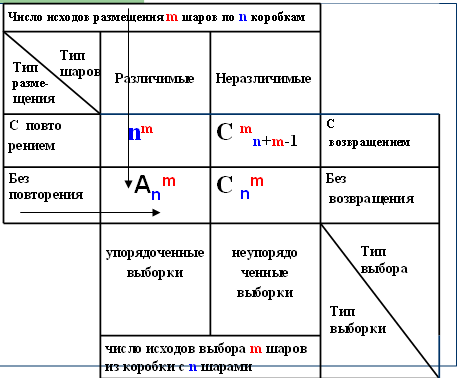
Рисунок 1. Таблица решения комбинаторных задач
Задача №1 (Н. Я. Виленкин Алгебра 9 кл., 1999 г. глава XIII № 1).
Учащиеся 9-го класса изучают 10 предметов. Сколькими способами можно составить расписание на один день так, чтобы было 6 различных уроков?
Решение – рассуждение детей.
1. Определим, какой модели соответствует эта задача.
Так как 6 из 10 предметов размещаются на места в расписании, то эта задача соответствует модели № 1. В таблице находим «Число исходов размещения m шаров по n коробкам». Это первая строка.
2. Определим тип размещаемых предметов.
Так как в расписании на день должны быть 6 различных уроков, то в таблице находим «Тип шаров», «Различимые». Это второй столбец.
3. Определим тип размещения.
В расписании не должны повторяться уроки, находим строку «Тип размещения», «Без повторения». Это четвертая строка.
4. На пересечении второго столбца и четвертой строки находим Аnm, n = 10, m = 6 (Рисунок 2). По формуле размещений находим количество способов составления расписания на один день 10 • 9 • 8 • 7 • 6 • 5 =151200.
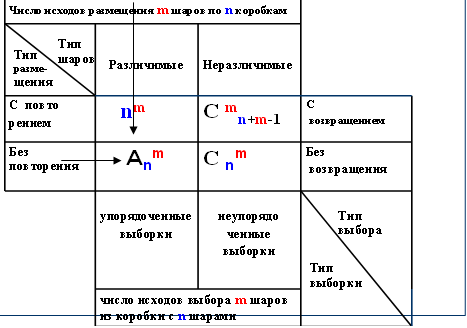
Рисунок 2. Иллюстрация решения задачи № 1
Задача № 2. (9.67.(а) Ю. М. Макарычев Н. Г. Миндюк Элементы статистики и теории вероятностей. Алгебра 7 – 9 классы, 2005г.)
В шахматном кружке занимаются 16 человек. Сколькими способами тренер может выбрать из них для предстоящего турнира команду из четырех человек?
Решение – рассуждение детей.
1. Определим, какой модели соответствует эта задача.
Так как тренер выбирает команду, состоящую из 4 человек, то эта задача соответствует второй модели – выборке. В таблице находим «Число исходов выбора m шаров из коробки с n шарами». Это шестая строка.
2. Определим тип выборки. Порядок выбора четырех человек «неважен», поэтому выборка неупорядоченная. В таблице находим «Тип выборки», «Неупорядоченные выборки». Это третий столбец.
3. Тип выбора в этой задаче «Без возвращений», так как команда состоит из четырех различных человек, повторений не будет. Это четвертая строка сверху.
4. На пересечении третьего столбца и четвертой строки находим Сnm, n=16, m= 4. (Рисунок 3). По формуле сочетаний находим количество выбора 4 человек из 16 в команду для шахматного турнира (1820).
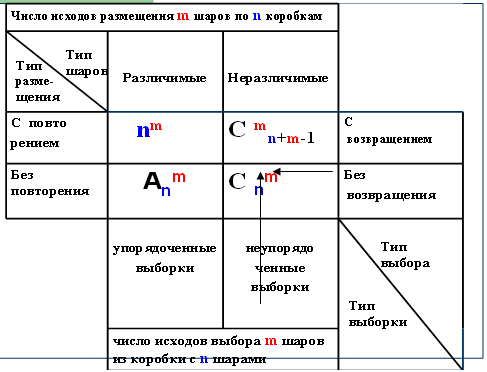
Рисунок 3. Иллюстрация решения задачи № 2
Задача № 3 (9.67.(б) Ю. М. Макарычев Н. Г. Миндюк Элементы статистики и теории вероятностей. Алгебра 7 – 9 классы, 2005г.).
В шахматном кружке занимаются 16 человек. Сколькими способами тренер может выбрать из них для предстоящего турнира команду из четырех человек, указав при этом, кто из членов команды будет играть на первой, второй, третьей и четвертой досках?
1. При решении этой задачи ученики также определяют соответствие условия задачи второй модели.
2. Однако порядок выбора 4 человек из 16 «важен», так как указывается, кто из членов команды будет играть на первой, второй, третьей и четвертой досках. Поэтому выборка упорядоченная. В таблице находим «Тип выборки», «Упорядоченные выборки». Это второй столбец.
3. Тип выбора такой же, как и в предыдущей задаче «Без возвращений». Это четвертая строка.
4. На пересечении второго столбца и четвертой строки находим Аnm, n = 16, m = 4. (Рисунок 4).
По формуле Аnm ученики находят количество способов выбора 4 членов команды из 16 человек для шахматного турнира 16 • 15 • 14 • 13 = 43 680.
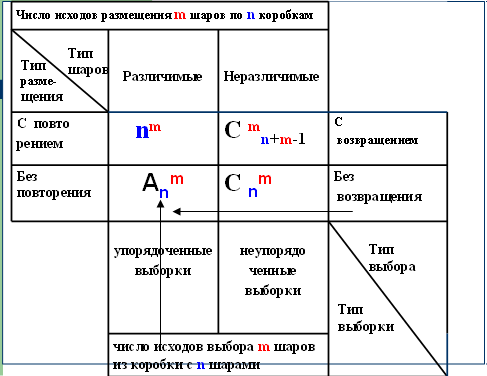
Рисунок 4. Иллюстрация решения задачи № 3
Решение этой задачи можно построить, используя другую модель: размещение m шаров по n коробкам.
Используя эту модель, обучающиеся находят первую строку «число исходов размещения m шаров по n коробкам. Это первая строка. Затем определяют «тип шаров» - члены команды относятся к «различимым шарам». Это вторая строка. И, наконец, по условию задачи один и тот же член команды не может занимать несколько мест сразу, поэтому тип размещения – «без повторения».
На пересечении второго столбца и четвёртой строки находим способ нахождения количества комбинаций размещения четырёх игроков из шестнадцати для участия в шахматном турнире , указав, кто из членов команды будет играть на первой, второй, третьей и четвертой досках: Аnm.
Учащимся очень удобно пользоваться таблицей решения, в ней заложены характеристики размещений и выборок, определяя которые, ученики могут безошибочно определять способ решения комбинаторных задач. Таким образом, таблица решения - это алгоритм решения комбинаторных задач.
Этот методический прием позволяет обучающимся моделировать задачи, классифицировать их по различным типам, а значит, формирует комбинаторную компетентность.