В предлагаемом материале для возможной в дальнейшем публикации хотелось бы поделиться практическим опытом решения тригонометрических неравенств с помощью формул решения простейших тригонометрических уравнений. Для решения тригонометрических неравенств чаще используется метод с использованием единичной окружности и графический метод с использованием графиков тригонометрических функций. Оба метода имеют свои недостатки. Графический метод достаточно громоздкий, занимает много времени на решение, так как для каждого неравенства требуется построение графика тригонометрической функции. В методе с применением единичной окружности вызывает затруднение учащихся определение и запись чисел в радианах, соответствующих точкам окружности, особенно если точки находятся не в первой координационной четверти.
Метод с использованием формул решения простейших тригонометрических уравнений даёт возможность избежать этих трудностей, кроме того, позволяет получить достаточно простой алгоритм решения неравенства.
С данной методикой решения познакомился в 1995 году на страницах журнала «Математика в школе» и с тех пор использую её в своей работе. Считаю её удобной и эффективной, а возможность знакомства с этой методикой и её использованием на уроке может быть практически полезной учителю, а содержание представленного урока послужит примером практической популяризации изложенной на страницах предметного журнала «Методики решения простейших тригонометрических неравенств».
2. Конспект урока (90 минут).
Цель: Научить решать простейшие тригонометрические неравенства с функциями sin x, cos x, используя формулы решения простейших тригонометрических уравнений.
Ход урока
1. Объявить цель урока. Провести повторение по схеме:
а) Вспомнить, как определяются в таблице arcsin a, arcos a.
б) Формулы
решения простейших тригонометрических уравнений sin x = a, cos x = a,
при ׀а׀ 1.
1.
в) Графическое толкование этих формул.
г) Как определяются корни уравнений по этим формулам.
Задание 1
Определить, работая по таблице (заранее подготовлено на доске)
|
arcsin |
arccos 1/2 = |
|
arcsin(- |
arccos (-1/2) = |
|
arcsin 1 = |
arccos |
|
arcsin (-1) = |
arcсos (- |
После выполнения задания целесообразно ответить на вопросы:
1. Каким образом определяется по таблице arcsin, arcсos числа по таблице?
2. Какие соответственно используются промежутки?
При ответе на второй вопрос необходимо добиваться формулировки теоремы о корне уравнения и напомнить учащимся, что х = arcsin a, х = arcos a являются соответственно корнями уравнений sin x = a, cos x = a на промежутках [-π/2; π/2] и [0; π].
Желательно иметь на доске рисунки № 65, 66 учебника А. Н. Колмогорова.
Задание 2
Записать
на доске формулы решения уравнений sin x = a, cos x = a при ׀а׀ 1.
1.
х = (-1)n
arcsin a + πn; n Z х = ± arccos a
+ 2πn; n
Z х = ± arccos a
+ 2πn; n Z
Z
(записывают учащиеся на доске).
Задание 3
Решить уравнения
sin x = 1/2 cos x = 1/2
Учащиеся решают на месте, затем у доски.
Задание 4
Определить для каждого из решённых уравнений х0, х1, х2.
Учащиеся определяют на местах, затем у доски. Трудность может вызвать определение корней для уравнения cos x = 1/2, поэтому следует обратить их внимание на особенность определения, о которой говорилось ранее на уроках решения простейших тригонометрических уравнений.
Задание 5
Вспомнить вместе с классом графическое толкование решения соответствующих уравнений, обратившись к графикам.
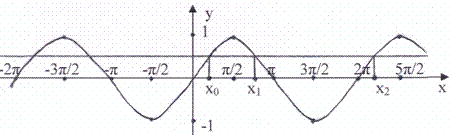
Рисунок 1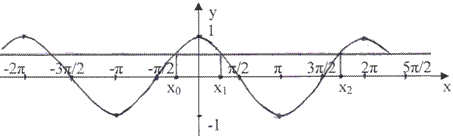
Рисунок 2
Графики выполнены заранее на закрытой части доски. При этом желательно определить для уравнения cos x = а, что х0 = - arcсos a, х1 = + arcсos a, х2 = - arcсos a + 2πn.
Для уравнения sin x = a, x0
= arcsin a, х1 = - arcsin a
+ π, х2 = arcsin a +
2π. Попытаться добиться от
учащихся ответа на вопрос «Что является графическим решением данных
уравнений?», а затем и неравенств с соответствующими функциями. Обратить
внимание на то, что для неравенств со знаком 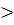 соответствуют интервалы
(х0, х1), со знаком
соответствуют интервалы
(х0, х1), со знаком  интервалы (х1,
х2), повторяющиеся через число, кратное периоду функции.
интервалы (х1,
х2), повторяющиеся через число, кратное периоду функции.
Проведя данное повторение, учащиеся готовы к восприятию нового материала, который можно начать с воспроизведения приводимого выше алгоритма решения неравенства с функцией sin x.
II. Новый материал
1. Алгоритм для неравенства sin х:
sin x  а
а
sin x 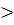 а
а
1)
Записать формулу решения sin x = а, при ׀а׀ 1.
1.
х = (-1)n∙arcsin
a + πn; n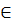 Z.
Z.
2) Для sin x 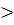 а найти х0,
х1, получая n = 0,1.
а найти х0,
х1, получая n = 0,1.
Для sin x  а найти х1,
х2, получая n = 1,2.
а найти х1,
х2, получая n = 1,2.
3) Записать ответ
Для sin x 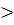 а
х0+2πn
а
х0+2πn х
х х1+2πn;
n
х1+2πn;
n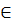 Z.
Z.
Для sin x  а х1+2πn
а х1+2πn х
х х2+2πn;
n
х2+2πn;
n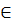 Z.
Z.
2. Алгоритм для неравенства cos х:
cos x 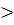 a
a
cos x  a
a
1)
Записать формулу решений простейшего уравнения cos x = а, при ׀а׀ 1.
1.
х = ± arccos a
+ 2πn; n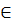 Z.
Z.
2) Для cos x 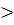 а найти х0,
х1, получая n = 0.
а найти х0,
х1, получая n = 0.
Для cos x  а найти х1,
х2, получая n = 0,1.
а найти х1,
х2, получая n = 0,1.
3) Записать ответ
Для cos x 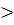 а х0+2πn
а х0+2πn х
х х1+2πn;
n
х1+2πn;
n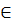 Z.
Z.
Для cos x  а х1+2πn
а х1+2πn х
х х2+2πn;
n
х2+2πn;
n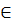 Z.
Z.
1. Затем следует совместно с учащимися отработать полученные алгоритмы.
Учитель решает совместно с учащимися неравенства.
Например: sin x 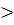 1/2 sin 2х
1/2 sin 2х 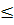 1/2
1/2
Желателен
разбор неравенств варианта 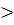 ,
,
 ,
, 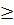 ,
, 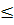 , а также с аргументом
отличным от «х», чтобы показать, как это изменит запись ответа, а именно:
замена скобок интервала на скобки промежутка и на количество корней в связи с
изменением аргумента, но при этом отметить, что на сам алгоритм это не
оказывает никакого влияния.
, а также с аргументом
отличным от «х», чтобы показать, как это изменит запись ответа, а именно:
замена скобок интервала на скобки промежутка и на количество корней в связи с
изменением аргумента, но при этом отметить, что на сам алгоритм это не
оказывает никакого влияния.
1) х =
(-1)n∙arcsin 1/2 + πn; n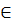 Z.
Z.
х = (-1)n∙π/6+πn; n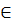 Z.
Z.
2) Для sin x 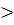 1/2
1/2
х0=(-1)0∙π/6+π∙0= π/6
х1=(-1)1∙π/6+π= 5π/6
3) Ответ:
π/6+2πn х
х 5π/6+2πn; n
5π/6+2πn; n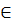 Z.
Z.
(π/6+2πn; 5π/6+2πn); n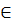 Z.
Z.
4. Предлагается самостоятельное решение на два варианта с последующим разбором и оценкой в случае успешного решения.
1 вариант, 2 вариант
sin x ≥ 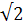 /2 sin x ≤ (-
/2 sin x ≤ (-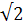 /2)
/2)
Разобрать решение у доски. При успешном решении оценить.
1 вариант может переписать решение неравенства 2 варианта и наоборот.
5. Записать алгоритм решения неравенства с функцией cos x.
Учитель записывает на доске, учащиеся – в тетрадях.
cos x 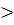 1/2
1/2
сos x 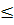 - 1/2
- 1/2
Например: cos (x/2) 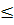 - 1/2
- 1/2
1) х = ± arcсos (-1/2) + 2πn; n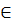 Z.
Z.
х = ±
(2π/3) + 2πn; n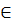 Z.
Z.
2) Для cos x 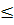 - 1/2
- 1/2
при n=0 х1 = + arсcos (-1/2) + 2π∙0= 2π/3
при n=1 х2 = - arcсos (-1/2) + 2π∙1= -2π/3+2p=4p/3
3) Ответ:
2π/3+2πn
≤ х/2 ≤ 4π/3+2πn; n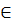 Z.
Z.
4π/3+4πn ≤ х ≤ 8π/3+4πn; n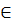 Z.
Z.
[4π/3+4πn; 8π/3+4πn]; n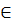 Z.
Z.
Аргумент х/2 выбран не случайно. При разборе неравенства с функцией sin x рассматривалось неравенство с аргументом 2х. При наличии времени на уроке можно обратить внимание учащихся, как зависит частота повторяемости интервалов решения неравенства в связи с изменением аргумента функции, а значит и деформации самого графика, тем более что вопрос о преобразовании графиков рассматривался ранее.
6. Предлагается самостоятельное решение на два варианта с последующим разбором и оценкой в случае успешного решения.
1 вариант, 2 вариант
cos x < (-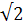 /2) cos x ≥
/2) cos x ≥ 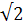 /2
/2
Разобрать решение у доски. При успешном решении оценить.
1 вариант может переписать решение неравенства 2 варианта и наоборот.
III. Закрепление материала
1. Повторить с учащимися ещё раз записанные алгоритмы, выяснить затруднения, которые им встретились при решении неравенств. Дать необходимые разъяснения.
2. Предложить учащимся самостоятельную работу на 10-15 минут.
Например:
|
1 вариант, |
2 вариант |
|
sin x ≤ |
sin x > |
|
cos 2x > 1/2 |
cos x/4 ≤ -1/2 |
В сильном классе работа может быть выполнена за 10 и менее минут, в среднем – достаточно 15 минут, если класс слабый, времени на самостоятельную работу может не остаться совсем, поэтому её можно провести в начале следующего урока. Самостоятельная работа даст возможность учителю посмотреть, как усвоен алгоритм, выделить основные трудности и ошибки, допущенные учащимися при решении, анализ которых проводится на следующем уроке.
IV. Домашнее задание
Объём и уровень сложности домашнего задания учитель определяет сам, исходя от того, как прошёл урок, насколько учащиеся, по его мнению, освоили алгоритм, от объёма сделанной на уроке работы.
V. Итог урока
При подведении итога урока учитель оценивает тех учащихся, которые активно работали на первом этапе урока при повторении материала, напоминает оценки, полученные учащимися при решении неравенств.
Необходимо, чтобы учащиеся вспомнили цель, поставленную в начале урока и его главный итог получения алгоритмов для решения неравенств с функциями sin x, сos x.
Примерное оформление доски для урока – Приложение 1.
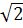 /2 =
/2 = 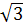 /2 =
/2 =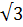 /2
/2