Класс: 11
Тип урока: Урок формирования знаний
Цели урока:
- познакомить обучающихся с новыми для них видами показательных неравенств, формирование знаний об основных методах решения показательных неравенств.
- развитие умений сравнивать, выявлять закономерность, обобщать, развитие логики, памяти.
- воспитание ответственного отношения к учебному труду
Этапы урока и их содержание
1. Организационный этап.
2. Постановка цели.
На уроке будут рассмотрены новые для обучающихся неравенства - показательные, решение которых требует хорошего знания теоретического материала. Данные неравенства ежегодно присутствуют в вариантах ЕГЭ по математике.
3. Актуализация знаний.
Теоретический опрос:
а) определение показательной функции;
б) какова область определения показательной функции;
в) какова область значений показательной функции;
г) в каком случае показательная функция является возрастающей, убывающей;
д) как расположен график;
е) каковы основные методы решения показательных уравнений (метод замены, однородное уравнение, разложение левой части уравнения на множители и переход к совокупности, функционально-графический, метод интервалов);
ж) что называется решением неравенства, что значит решить неравенство.
4. Введение знаний.
1) Простейшие показательные неравенства имеют
вид ![]()
![]() решений не
имеет, а неравенство
решений не
имеет, а неравенство ![]() выполняется при всех значениях
аргумента, поскольку
выполняется при всех значениях
аргумента, поскольку ![]() (Рассказ сопровождается графической
иллюстрацией)
(Рассказ сопровождается графической
иллюстрацией)
При ![]() выполняется равенство
выполняется равенство ![]() . Если
. Если ![]() , то в силу возрастания показательной
функции неравенство
, то в силу возрастания показательной
функции неравенство ![]() выполняется при
выполняется при![]() , а неравенство
, а неравенство![]() выполняется при
выполняется при ![]() . (Рассказ
сопровождается графической иллюстрацией)
. (Рассказ
сопровождается графической иллюстрацией)
Если ![]() , то в
силу убывания показательной функции неравенство
, то в
силу убывания показательной функции неравенство![]() выполняется
при
выполняется
при ![]() а
неравенство
а
неравенство![]() выполняется при
выполняется при ![]() . . (Рассказ сопровождается графической
иллюстрацией)
. . (Рассказ сопровождается графической
иллюстрацией)
Рассмотреть примеры: ![]()
Используя свойство монотонности показательной
функции делаем вывод, что неравенство ![]() при
при![]() равносильно
неравенству
равносильно
неравенству ![]() а при
а при ![]() равносильно неравенству
равносильно неравенству ![]()
2) Рассмотрим методы решения показательных неравенств, не являющихся простейшими. При их решении используются приёмы преобразования выражений, стоящих в левой и правой частях неравенства, аналогичные тем, которые использовались и при решении показательных уравнений.
а) Метод замены переменной. В этом случае новая неизвестная подбирается так, чтобы относительно неё неравенство не было показательным.
Пример 1: Сведение к квадратному неравенству.
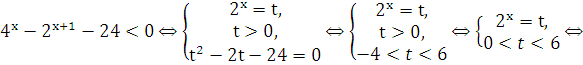
![]() .
.
Ответ: ![]()
Пример 2: Сведение к рациональному неравенству, которое решаем применяя метод интервалов для непрерывных функций.
![]()
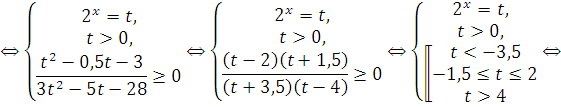
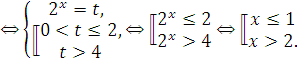
Ответ: ![]()
б) Решение однородных неравенств. При решении
однородных неравенств используется свойство
показательной функции ![]() , производим деление обеих частей
неравенства на положительную величину и вводим
новую переменную. Однородное неравенство первой
степени
, производим деление обеих частей
неравенства на положительную величину и вводим
новую переменную. Однородное неравенство первой
степени ![]() +n
+n![]() решается
делением обеих частей неравенства на
решается
делением обеих частей неравенства на ![]() , а однородное
неравенство второй степени
, а однородное
неравенство второй степени ![]() решается делением на
решается делением на ![]()
Пример: ![]()
Решение:
![]()
Так как ![]() для
любых x, то разделив обе части неравенства на
для
любых x, то разделив обе части неравенства на ![]() , получим
неравенство, равносильное данному:
, получим
неравенство, равносильное данному:
![]() -
-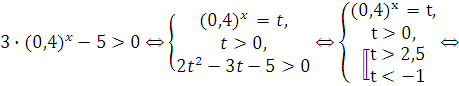
![]()
Ответ: (-![]()
в) Метод интервалов.
Пример:
![]()
Решение.
Рассмотрим функцию f(x)![]() , областью определения которой
является множество неотрицательных чисел.
Находим нули функции, решив уравнение
, областью определения которой
является множество неотрицательных чисел.
Находим нули функции, решив уравнение ![]() . Делим обе
части уравнения на
. Делим обе
части уравнения на ![]() , после преобразований получим
уравнение
, после преобразований получим
уравнение
![]() откуда
откуда ![]() Последнее
уравнение не имеет решения, а уравнение
Последнее
уравнение не имеет решения, а уравнение ![]() имеет
единственный корень, равный 4. Нуль функции
разбивает область определения на промежутки
имеет
единственный корень, равный 4. Нуль функции
разбивает область определения на промежутки ![]() и
и![]() , в которых функция (в силу
своей непрерывности) сохраняет знак.
, в которых функция (в силу
своей непрерывности) сохраняет знак.
f(1)![]()
![]() f(9)
f(9)![]()
Итак, исходное неравенство выполняется при ![]()
Ответ:![]()
г) Функционально-графический метод.
Пример: ![]()
Решение. Функции ![]() и
и![]() определены
на всём множестве действительных чисел. Функция
определены
на всём множестве действительных чисел. Функция ![]() возрастающая на
R, а функция
возрастающая на
R, а функция ![]() убывающая на R, значит, уравнение
убывающая на R, значит, уравнение ![]() имеет не более одного
корня. Не сложно убедиться в том, что 1 является
единственным корнем уравнения. Таким образом,
графики функций имеют одну точку пересечения.
Неравенство имеет решение тогда, когда график
функции
имеет не более одного
корня. Не сложно убедиться в том, что 1 является
единственным корнем уравнения. Таким образом,
графики функций имеют одну точку пересечения.
Неравенство имеет решение тогда, когда график
функции ![]() лежит не выше графика функции
лежит не выше графика функции ![]() то есть при
то есть при ![]()
Ответ: (![]()
5. Первичное осмысление изученного.
Из предложенных неравенств выбрать наиболее рациональный способ для их решения:
а) ![]()
Ответ: однородное неравенство, делим обе части,
например, на ![]() и введение новой переменной
и введение новой переменной ![]() .
.
б)![]()
Ответ: с помощью замены ![]() сводим к решению
дробно-рационального неравенства.
сводим к решению
дробно-рационального неравенства.
в) ![]()
Ответ: решается функционально-графическим способом.
г) ![]()
Ответ: использование свойства монотонности показательной функции.
6. Подведение итогов обучения. Домашнее задание и его инструктаж (конспект, неравенства из пункта 5)