Цели:
Образовательные: cформировать понятие линейного уравнения с одной переменной, закрепить знания обучающихся по данной теме с использованием алгоритма решения линейного уравнения.
Развивающие: развивать умения пользоваться опорным конспектом и вспомогательной литературой для постановки задачи и ее выполнения в ходе решения уравнений; развивать внимательность, собранность и аккуратность; развивать умения работать самостоятельно и в микро группах, ставить перед собой цель и делать выводы, выполнять безошибочно необходимые арифметические вычисления.
Воспитательные: воспитывать внимательность учащихся, создание позитивного отношения учащихся к изученному разделу, умения ясно и четко излагать свои мысли, способствовать математической и общей грамотности.
Ход урока
«Уравнение представляет собой наиболее серьёзную и важную вещь в математике».
Лодж О.
I. Организационный момент.
– Сегодня на уроке мы познакомимся с понятием линейного уравнения с одной переменной; рассмотрим алгоритм решения уравнения. Девизом нашего урока будут слова английского физика и изобретателя Сэра Оливера Джозефа Лоджа.
II. Актуализация знаний.
Учитель проводит устное тестирование.
Выберите строку, в которой записано уравнение:
Какое из чисел является корнем уравнения –2х = 24?
Для какого из уравнений число –2 является корнем?
Приведите подобные слагаемые: 3а + 2а + 4а – 7а
Равносильны ли уравнения: –2(х - 4) = 4 и 2(х - 4) = –4
|
В ходе тестирования обучающимся предлагает ответить на вопросы:
– Что называется уравнением?
– Что называется корнем уравнения?
– Что значит решить уравнение?
– Какие уравнения называются равносильными?
III. Изучение нового материала.
Учитель предлагает обучающимся из списка выбрать уравнения вида ах =b
- -0,8x2 =48;
- -1,2х=-3,6;
- 5x2-3х=0;
- 6у=2,4;
- 3z=-9
| 2(8 – х) = 10 | Раскрыть скобки в обеих частях уравнения |
| 16 – 2х =10 | Перенести слагаемые, содержащие переменнуюв одну часть, а не содержащие – в другую |
| –2х = 10 – 16 | Привести подобные слагаемые в каждой части |
| –2х = –6 | Разделить обе части уравнения на коэффициент переменной |
| х = 3 |
Затем дает определение линейного уравнения с одной переменной и рассматривает алгоритм решения уравнения.
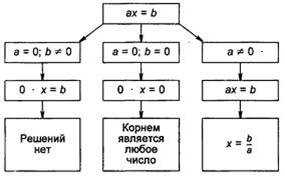
Учитель предлагает обучающимся выяснить, сколько корней может иметь данное уравнение. Для этого составляют опорный конспект.
Затем учитель разбирает решение линейных уравнений, используя опорный конспект:
- 4(х + 7)= 3 - х;
- 2х + 5= 2(х + 10);
- 4(х + 3)= 2(х + 6) + 2х
Проводит физкультминутку:
Рисуй глазами треугольник
Рисуй глазами треугольник.
Теперь его переверни
Вершиной вниз.
И вновь глазами
ты по периметру веди.
Рисуй восьмерку вертикально.
Ты головою не крути,
А лишь глазами осторожно
Ты вдоль по линиям води.
И на бочок ее клади.
Теперь следи горизонтально,
И в центре ты остановись.
Зажмурься крепко, не ленись.
Глаза открываем мы, наконец.
Зарядка окончилась.
Ты – молодец!
IV. Первичное закрепление изученного материала.
Учитель предлагает обучающимся выполнить задание на доске и в тетрадях.
Задание. Используя опорный конспект, решите уравнения:
- 4(х + 5) = 5(х + 4) – х
- 6х + 3 = 6(х + 5)
- 8х + 4 = 2х + 22
- –12n – 3 = 11n – 3
Обучающиеся на уроке продолжают работу в группах:
1 группа работает самостоятельно, выполняя № 130(в), 132(б, г), один ученик – за доской.
2 и 3 группы – совместно выполняют задание на доске и в тетради №128(а, б, в), 130 (а, е).
Затем 2 и 3 группе учитель предлагает выполнить обучающийся тест, а с 1 группой осуществляет проверку № 130(в), 132 (б, г).
Тест 2 и 3 группе:
| Задание 2 группе | Задание 3 группе |
| 1. Укажите уравнение, которое не является линейным уравнением с одной переменной | |
|
|
| 2. Решите равнение | |
0, 8х – (0, 2х + 4) = 2
|
0,3х – 0,45 =0
|
| 3. Сколько корней имеет уравнение? | |
4х + 3 = 5 + 4( х – 2)
|
2х + 3 = - 6
|
| 4. Найдите корни уравнения | |
|
|
| 5. Найдите значение а, при котором равны значения выражений | |
–15а + 8 и –17а – 12
|
4а – 2 и а + 4
|
Затем учитель разбирает с 1 группой решение линейных уравнений с параметром.
Задание 1. При каком а уравнение 2ах + 5 = 3х имеет корень, равный –1?
Задание 2. При каких а уравнение 6(ах – 1) + а = 3(а – х) +7 имеет бесконечно много корней?
Задание 3. При каких а уравнение 2(3х – 2а) = 2 + ах не имеет о корней?
А группа 2 и 3 проверяет решение теста с помощью готовых ответов.
| 2 группа. Ответы. 13442 | 3 группа. Ответы. 42113 |
V. Домашнее задание
Учитель предлагает каждому обучающемуся:
1. Карточку для работы с текстом параграфа по плану:
|
2. Дифференцированное домашнее задание по группам:
1 группа №132 (б, г), №138
2 группа №129 (в, ж, г), №133 (б, в)
3 группа №126 (а, г, ж), №128 (г, д)
VI. Итог урока.
Итак, что нового сегодня Вы узнали на уроке?
Дайте определение линейного уравнения. Сколько корней может иметь линейное уравнение? Приведите примеры линейных уравнений с одной переменной.